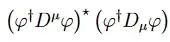This document https://arxiv.org/abs/1008.4884
presents in Tables 2 and 3 the mathematical expression of many dimension-6 operators,
for example (just an example)
The mathematical expression does not help so much to visualize the corresponding expression (in particular those who have a derivative).
Are there Feynman diagrams for dimension 6 operator ? or is drawing Feynman diagram for that does not make sense ?
Of course drawing Feynman diagrams for such vertices makes sense. (I'm leaving the meaningfulness of loop corrections for nonrenormalizable interactions aside; these are effective field theory terms.)
For example, a term $(\phi^\dagger \phi)^3$ amounts to a plain vertex with six incoming scalar field lines.
The fGGG term trilinear in gauge field strengths, includes diagrams with six gauge fields, or lesser numbers, supplanting momenta for gauge fields, etc.
The term you wrote has several Feynman diagrams corresponding to its pieces: the easiest one has four scalars and two gauge fields coming in; there is one with four scalar fields, and two suitable momenta with the right symmetries for the "kinetic-like" term, and mixed terms with four scalars, one momentum and one gauge field. And so on...
The textbook Feynman rules are identical in this case. It's what you would do with the answers that bears further discussion, judiciously excluded here.
