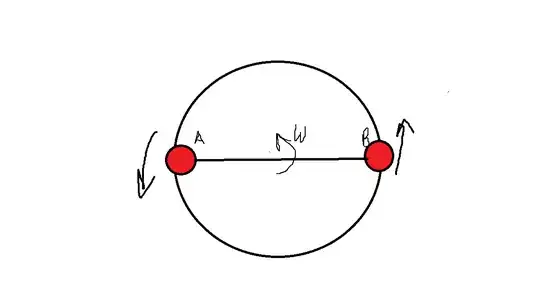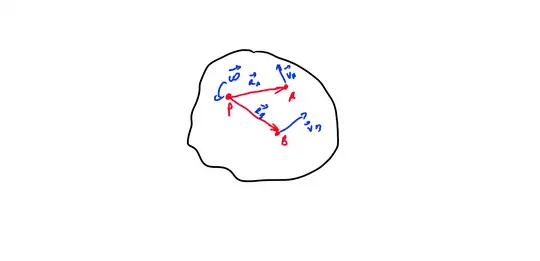
The relative angular velocity$~\vec{\omega}_{r}~$ can obtain from this equation:
$$\vec{\omega}_{r}=\frac{\vec{R}_{AB}\times \vec{V}_{AB} }{\vec{R}_{AB}\cdot \vec{R}_{AB}}\tag 1$$
with :
$$\vec{R}_{AB}=\vec{R}_{B}-\vec{R}_{A}$$
$$\vec{V}_{AB}=\vec{V}_{B}-\vec{V}_{A}$$
equation (1)
$$\vec{\omega}_{r}=\frac{\left(\vec{R}_{B}-\vec{R}_{A}\right)\times \left(\vec{V}_{B}-\vec{V}_{A}\right) }{\vec{R}_{AB}\cdot \vec{R}_{AB}}\tag 2$$
with $~\vec{V}_A=\vec{\omega}\times \vec{R}_A~$ and
$~\vec{V}_B=\vec{\omega}\times \vec{R}_B~$
equation (2)
$$\vec{\omega}_{r}=\frac{\vec{R}_{AB}\times (\vec{\omega}\times \vec{R}_{AB})}{\vec{R}_{AB}\cdot \vec{R}_{AB}}=\frac{(\vec{R}_{AB}\cdot \vec{R}_{AB})\vec{\omega} - ( \vec{R}_{AB}\cdot \vec{\omega})\vec{R}_{AB}}{\vec{R}_{AB}\cdot \vec{R}_{AB}}\tag 3$$
Now if A and B lie in the plane perpendicular to ω then $$\vec{R}_{AB}\cdot \vec{\omega} = \vec{0}$$
equation (3) becomes:
$$\vec{\omega}_{r} = \frac{(\vec{R}_{AB}\cdot \vec{R}_{AB})\vec{\omega}}{\vec{R}_{AB}\cdot \vec{R}_{AB}} = \vec{\omega}$$
thus the relative angular velocity is ω.