Conceptual confusion about the relative angular velocity of particles in a rigid body

Question

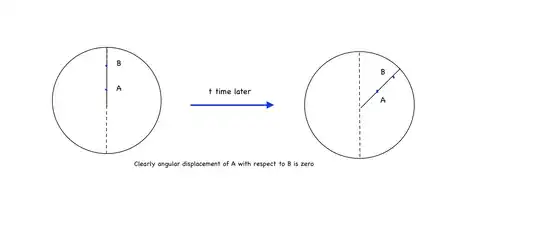
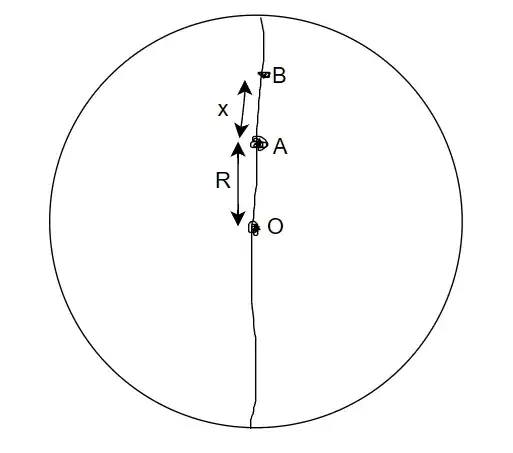
Let me explain my doubt with help of an example consider a disc of radius $2R$ rotating with contant angular velocity $\omega$ locate two particles $A$ at a distance $R$ from centre and $B$ at a distance $2R$ from the centre, we know that $\omega_A=\omega$ and $\omega_B=\omega$ ,Also $v_A=R\omega$ and $v_B=2R\omega$ , now $\omega_{B/A}=\dfrac{v_{B/A}}{r_{B/A}}=\omega$ but if I use the definition $\omega=\dfrac{d{\theta}}{dt}$ we get a contradicting result, $\omega_{B/A}=\dfrac{d{\theta}}{dt}=0$ since $\theta$ is the angle between the line joining them which does not change with time. My doubts

1. Is $\omega=\dfrac{d{\theta}}{dt}$ always valid , even for rotating frames, If yes how do I derive ralative angular velocity between the two particles only using this definition?
2. Am I making any conceptual error?

EDIT 1 : For a rigid body we can say each point turns relative to other point of the rigid body with same angular velocity at a given instant. So $\omega_{B/A}$ is indeed equal to $\omega$.Then why the contradiction occurs?

EDIT 2: https://www.brown.edu/Departments/Engineering/Courses/En4/notes_old/RigidKinematics/rigkin.htm Please check this link and see under 5.1.3 section where they derive equations governing general plane motion , there also they have used $\omega _{B/A}= \omega$ of the rigid body where A and B are any two arbitrary points.

EDIT 3: See that the equation $v_{A}=v_{B}+\omega_{B/A}×r_{A/B}$ where $\omega_{B/A}=\omega$ furthermore if we transform the equation we can se $v_{B}=v_{A}+\omega×r_{B/A}$ hence cocluding my point that $\omega_{B/A}=\omega_{A/B}=\omega$

EDIT 4: you can also see what I am trying to say here https://en.m.wikipedia.org/wiki/Angular_velocity under Rigid Body Consideration , Consistency.

EDIT 5: Here are some more links to support $\omega_{B/A}=\omega$

1. Relative angular velocity of point with respect to another point
2. Angular velocity about an arbitrary point

"Consider a rigid body rotating with angular velocity $\omega$ . Now, we know that this $\omega$ is an intrinsic property for the rigid body, in the sense that: Each point on the rigid body rotates with $\omega$ relative to any other point on the rigid body."

3. Relative angular velocity

4. "An important feature of spin angular momentum is that it is independent of the coordinate system. In this sense it is intrinsic to the body; no change in coordinate system can eliminate spin, whereas orbital angular momentum disappears if the origin is chosen to lie along the line of motion." , Source: An introduction to mechanics Textbook by Daniel Kleppner and Robert J. Kolenkow.

Answer 1

The mistake here is in the fundamental definition of relative angular velocity.

The relative angular velocity of B with respect to A is defined as : $$\omega_{BA}=\omega_B-\omega_A$$ Since $v=r\omega$ we can say $$\omega_{BA}=\frac{v_B}{r_b}-\frac{v_A}{r_A}$$ which is very different from $\frac{v_{BA}}{r_{BA}}$ mathematically.

On evaluating $\omega_{BA}=\frac{v_B}{r_b}-\frac{v_A}{r_A}$ we get the answer zero which is consistent with the results given by $\omega = \frac{d\theta}{dt}$. Thus the definition $$\omega = \frac{d\theta}{dt}$$ is absolutely correct.

EDIT

In the link attached it says: " We will examine the motion of this body in both, the fixed reference O shown, as well as relative to a non-rotating reference attached to point B." This means that the rotation of the body is about the point B. So $\omega_{B}$ is practically zero while $\omega_{A}$ is equal to $\omega$.Then $$\omega_{AB}=\omega_{A}-\omega_{B}$$$$\omega_{AB}=\omega-0= \omega $$

But if you considered the scenario I have introduced in the diagram where the rotation neither about point A or B but about the centre, the results are consistent with my explanations.

For another intuitive understanding think of how the Earth rotates about its axis but to us everything appears to be at rest at all times.

Answer 2

θ is measured in the fixed reference system, even if measured between the two points A and B it changes when the disc rotates: it is not zero.

however, wrt the rotating reference system of the disc itself the angular velocity of the points of the disc is zero because the disc is rigid... if the disc was "soft" or a fluid, the things would be different and may follow a vortex with non uniform angular velocities.

Answer 3

for anyone in the future looking for an answer the relative angular velocity of the particles in a rigid body are indeed 0 since well the body is rigid and all the particles undergo same angular displacement (if the angular velocity would be different it would be like a ring rotating about another ring) so anyway what the particles do have is relative linear velocities more specifically "relative tangential velocity" this is purely becoz of geometrical factors.

for example lets take two points A and B on a rigid disk rotating with angular velocity W, such that A,B and center of disk O lie on the same line, let the distance of point A from O be R and the distance between A and B be x

excuse the poor diagram

now Va = RW and Vb = (R+x)W (these are relative to the center)

so, $V_b$$_/$$_a$ = (R+x)W - RW = xW this is the linear velocity of B wrt to A NOT the relative angular velocity (also angular velocity of both A and B is W even though they have different velocities as they are at different distances from O and have to "travel" with different velocities to "cover" the same angle wrt the center O the cause is purely geometrical)

and now if we divide $V_b$$_/$$_a$ with there relative distance lets call is $S_b$$_/$$_a$ we get

$V_b$$_/$$_a$ / $S_b$$_/$$_a$ = W which is correct as per the textbooks

now one could argue that since B has a tangential velocity relative to A then it would also have a relative angular velocity wrt A ie $W_b$$_/$$_a$ = xW this is where the confusion lies as it doesnt make much physical sense but is widely used to make calculations simpler as we can take the angular velocity of the body about any particle to be the same as about its axis of rotation (most commonly used if AOR isnt passing through COM) so, i guess its more of a mathematical relation rather than the property of the system.

on a side note though if you are wondering what if A and B dont lie on the same line as show then what ? well then we would have to utilize vectors as direction of the velocities would be different but the result would still be the same.

EDIT

now that i think about it angular velocity is defined as below

W = d$\Theta$/dt

implying there must be a change in $\Theta$ so, $W_b$$_/$$_a$ = xW isnt correct as there isnt any change in $\Theta$ rather how i imagine it is if we paused time and then compared velocities we can there is a relative angular velocity equal to $\frac{V_{ tangential}}{R}$ = W