Frustration with Newton's Third Law of Motion

Question

from this morning I think about the third law of Newton and the force of buoyancy and I can't solve it. I know that I misunderstood something, but I can't find out what is it. And sorry if my questions are ambiguous, but I'm too tired, I want to find out where I'm wrong. these are my questions:

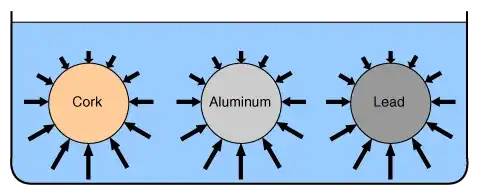
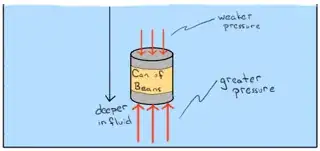
1. Why the Buoyancy Force= Force of the liquid that pushes the object upward (F2) - Force of the liquid that pushes the object downward(F1), what is measuring this buoyancy force. (What is trying to find with this operation F2-F1? )

2. When an object is in the water it pushes the water downward and at the same time, the water pushes the object upward with the same force (gravity) (Newton's Third Law). Then why we compare mg with Buyouncy force to see if is it floating (why we don't compare F2 (upward) + mg (normal force) with f1 (downward). (It was easier when I don't know the third law of motion because I thought only there is mg (gravity force)

Thank you for reading this and helping me to find the mistakes that I made (and sorry for my English :)

Edit: Now I want to know only why the buoyancy force= the force on the bottom - the force on the top

Answer 1

I'm not exactly sure if I understand the question so feel free to correct me if I misunderstood but here goes. Everytime a surface touches a liquid the liquid exerts a pressure on that surface. Pressure is just a force but exerted over a tiny area. Pressure rises with depth because each parcel of liquid has to hold up all the liquid above it. Specifically $p-p_s=\rho \cdot g\cdot h$ where $p$ is the pressure, $p_s$ is the pressure at the surface, $\rho$ is the density of the liquid, $g$ is gravitational acceleration and $h$ is the depth of the liquid measured from the surface.

If you draw the pressure that is exerted for submerged objects it looks like this:

Here you can see the pressure gets larger as you get deeper. To get the total bouyant force you have to add up all the little forces. Using calculus you can show that this force is equal to $$F_{buoyant}=\rho gV.$$ Here $\rho$ is again the density of the liquid and $V$ is the volume of the submerged object. This is the same as Archimedes' principle which says the buoyant force is equal to the weight of the water that the object displaces.

Surprisingly (maybe this isn't surprising to you) this force doesn't depend on the mass of the object, only on its shape. As pointed out in the picture the buoyant force is the same for a sphere made out of cork, aluminum or lead (if they have the same shape).

As to your question: why is the buoyant force the force of the liquid that pushes the object upward minus the force that is directed downward? Note that this is only correct for objects that are flat on the top and bottom like the can of beans below. The force on the top and bottom are along the same direction so you can just subtract them. To add forces that are not along the same direction you can use vector addition.

source of first image: http://hyperphysics.phy-astr.gsu.edu/hbase/pbuoy.html source of second image: https://www.khanacademy.org/science/physics/fluids/buoyant-force-and-archimedes-principle/a/buoyant-force-and-archimedes-principle-article

Note: to go from pressure to force you have to multiply by the area over which the pressure act $F=p\cdot A$. This equation only works if the area is small enough that the pressure is the same over the entire area.

Answer 2

Why the Buoyancy Force= Force of the liquid that pushes the object upward (F2) - Force of the liquid that pushes the object downward(F1), what is measuring this buoyancy force. (What is trying to find with this operation F2-F1? )

The buoyancy force is just the force that pushes the object upward. That force is

$$F_{buoyancy}=V_{l}ρ_{l}g$$

$V_l$ is the volume of the liquid displaced by the submerged volume of the object, $ρ_{l}$ is the density of the liquid (or specific gravity of the liquid), and $g$ is the acceleration due to gravity near the earth's surface.

The downward force on the object is the total weight of the object which equals

$$V_{o}ρ_{o}g$$

Where $V_o$ is the total volume of the object, not necessarily the submerged volume of the object, $ρ_{o}$ is the density of the object (or specific gravity of the object) and $g$ is again the acceleration due to gravity near the earth's surface. If the weight of the object is greater than the weight of an equal volume of the liquid, the object will sink.

In order for an object to float, regardless of how much is submerged, the net vertical force on the object has to be zero. That means the downward weight of the object must equal the upward buoyant force on the object. Or

$$V_{o}ρ_{o}g=V_{l}ρ_{l}g$$

The fraction of the object submerged is the ratio of the volume of the liquid displaced, $V_l$ to the total volume of the object, $V_o$ or

$$\frac{V_l}{V_o}=\frac{ρ_o}{ρ_l}$$

Bottom line: If the density (or specific gravity) of the object equals the the density (or specific gravity) of the liquid, the object will float completely submerged. If the density of the object is less than the liquid, it will float partially submerged.

Hope this helps.