1

I wanna consider some cases and make sure if im right ,

if i have fixed volume balloon filled with helium , and let balloon fly in air ,

1)

if air temperature increases , ( without increasing temp of helium ) that will decrease density of air , so buoyancy force decreases.

2)

but if helium temperature increase , volume is constant so pressure increases then helium density is constant , and density of air decreases so the buoyancy force decreases .

3)

but if volume of helium increases with constant pressure , helium density decreases , air density decreases so no effect .

So buoyancy force for immersed body contained contained fluid decreases with increasing temperature if temperature of internal fluid is insulated or constant volume , buoyancy force will not change with changing temp if volume change .

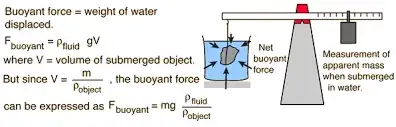[enter image description here]

ive read this answer here

Why do helium balloons rise and fall?

but i see different cases when volume of helium constant , as air density decreases so buoyancy force will decrease

Qmechanic
  • 220,844
Ahmed elmenshawie
  • 73

2 Answers2

0

You seem to have a misconception with the relationship between air density and buoyant force.

When the air density decreases and helium density stays the same, the buoyant force on the balloon is less. The way buoyancy works, the object with lower density floats until it approximately matches the density of it's surroundings. If the surroundings become less dense, than the force on the balloon becomes lower, and it sinks. If the air becomes more dense, it's the opposite.

I'm not sure if that fully answers what you are trying to figure out; but mixing up the effects is likely to cause confusion so it's important to clear up.

JMac
  • 15,595
0

The net buoyancy force is given by the difference in the weight of helium and that of air in the same volume, so

$$F_b=g(\rho_{air}V-\rho_H V)=\Delta\rho\; V g$$ where $\rho$ is density of air (helium) and $V$ the volume of your balloon.

In a first approximation, you can use the perfect gas law for helium $$pV=nRT$$ with $n$ constant ($R$ the gas constant, $p$ the pressure and $V$ the volume, changing depending on whether the volume is fixed or not) so that the density of helium is given by

$\rho_H=nM_H/V=pM_H/RT$ where $M_H$ is the molas mass of Helium.

On the other hand, the air density can be approximated by $$\rho_a=\rho_0(1-\tau h/T_0)^{\alpha g/\tau}$$ where $\alpha$ is a constant, $T_0$ is the temperature at sea level and $\tau$ the rate in change of temperature depending on height.

So your buoyancy becomes

$$F_b=g V(rho_a-\rho_H)=g V \left( \rho_0(1-\tau h/T_0)^{\alpha g/\tau} - p(h) M_H/RT(h) \right)$$ with $T(h)$ and $p(h)$ depending on the height.

Again, we can assume that $T(h)=T_0-\tau h$ and $$p(h)=p_0(1-\tau h/T_0)^{\alpha g/\tau}$$ (see link above) then you can plug in the numbers you have, the model you have for your balloon etc to see what direction the buoyancy points at at different heights

$$F_b=g V \left(1-\tau h/T_0\right)^{\alpha g/\tau}(\rho_0-p_0M_H/R(T_0-\tau h))$$

all of this also assumes that the helium immediately takes the temperature of the sorrounding and that the balloon is not so rigid that it is in equilibrium with the outside pressure. Again, you need to chage things depending on whether your balloon has constant volume, density, pressure etc.

JalfredP
  • 4,954