I'm doing some exercises on $LS$ coupling during my self-study of atomic physics. I understand how to construct a table of possible microstates. I also understand how to map term symbols to those cells of microstates: the total wave function must be antisymmetric under exchange of both electrons. Combining the fact that the parity of the spatial wave function is $(-1)^L$, spin singlets yield an antisymmetric spin wave function and spin triplets yield a symmetric spin wave function then allows me to determine the possible term symbols.
Now how does this work when there are more than 2 electrons? I know the wave function must still be antisymmetric under exchange of any two electrons. My notes contain the following tables:
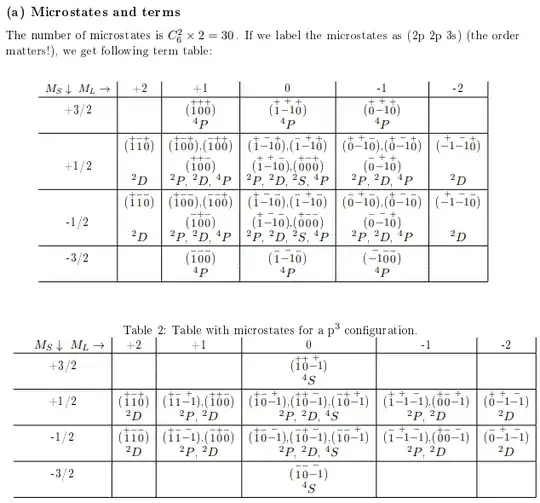
The first table is for a $2p^23s^1$ configuration, the second table for a $np^3$ configuration. I still understand how to figure out all possible microstates, but I can't seem to figure out which term symbols are allowed. Take for example the $M_L=0$, $M_S=3/2$ cell in the second table. I would say the spatial wave function is symmetric since $L=0$ and the spin wave function is symmetric as well since all spins are the same. So the total wave function is symmetric, which obviously can't be right. What am I doing wrong here?
Any help would be greatly appreciated!