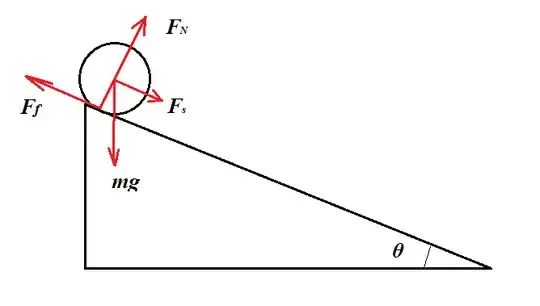
This not as banal a problem as you may expect at first sight.
First, study the emerging rotational motion:
$$F_N=mg\cos\theta$$
$$F_f=\mu_k F_N=\mu_k mg\cos\theta$$
Torque about the axis of rotation causes angular acceleration:
$$\tau=I\alpha$$
$$F_f R=I\frac{\text{d}\omega}{\text{d}t}$$
$$\mu_k mg\cos\theta R=\gamma mR^2 \frac{\text{d}\omega}{\text{d}t}$$
where $\gamma$ is a coefficient depending on the exact shape of the rotating body.
$$\frac{\text{d}\omega}{\text{d}t}=\frac{\mu_kg\cos\theta}{\gamma R}$$
Assuming $\omega =0$ at $t=0$:
$$\omega(t)=\frac{\mu_kg\cos\theta}{\gamma R}t$$
Now study the translational motion:
$$F_s-F_f=ma$$
$$mg\sin\theta-\mu_k mg\cos\theta=ma$$
$$\frac{\text{d}v}{\text{d}t}=g(\sin\theta-\mu_k \cos\theta)$$
Assuming $v=0$ at $t=0$:
$$v(t)=g(\sin\theta-\mu_k \cos\theta)t$$
The object reaches rolling without slipping (pure rolling) when:
$$v(t)=\omega(t)R$$
which with some substituting and reworking gives the relationship:
$$\mu_k=\frac{\gamma}{\gamma+1}\tan\theta$$
So how to calculate the relevant energies?
You already know the work done by the friction force.
How much energy is used to get the object to roll? Calculate the time needed to reach the bottom of the incline ($0 \to L$) and from there calculate $\omega(t)$ and use that to calculate the change in rotational kinetic energy.
I hope this helps.
