I'm trying to understand a passage from the paper "Gaussian operator bases for correlated fermions", J. F. Corney and P. D. Drummond (https://arxiv.org/abs/quant-ph/0511007), specifically going from the first to second line of Eq. (2.5), which is about Gaussian density operators:
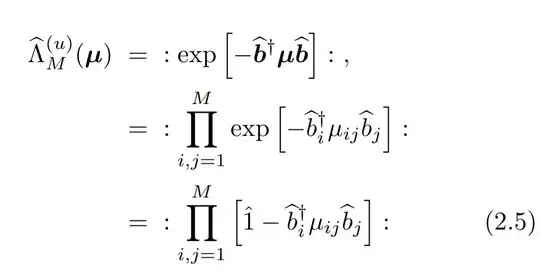
The operators $\hat{b}_i$ are fermionic, and so obey the usual anticommutation relations. The problem is, the term $\hat{b}_i^\dagger\hat{b}_j$ does not necessarilly commute with $\hat{b}_k^\dagger\hat{b}_l$, so I don't see how you can take the summation out of the exponential as a simple product. From the BCH formulas (https://en.wikipedia.org/wiki/Baker%E2%80%93Campbell%E2%80%93Hausdorff_formula), I would expect there to be another term that takes into accout the commutators $[X,Y]$, $[X,[X,Y]]$, etc.
Can someone shed some light into why are those terms zero/not necessary in this situation?