Setup: an official ping pong ball is floating inside a party plastic cup filled with clean water, which is then dropped from a certain height onto a soft mat.
Observation: the ping pong ball shoots up to a height which is much higher than its initial position.
Question: why does the ping pong ball do that? Why didn't the water and soft mat absorb the kinetic energy? Is this an inelastic collision?
PS: the first time it was an accident, the second time the soft mat and I were thrown out XD
I've confirmed the experiment, using a McD_n_lds paper drinks cup and a beer can hollow plastic ball of about $5\mathrm{g}$, of about the same diameter as a ping pong ball (PPB):
The observed effect depends largely on the cup being soft and permanently deformable (like an object made of blutack or playdough), so its collision with Earth is inelastic. A stiff, hard cup (made of steel e.g.) would not work the same way here. The inelastic collision of the ensemble causes kinetic energy of cup and water, post-collision, to be small.
The PPB bounces back quite high (from a quarter-filled cup) and the cup of water loses quite little water and doesn't really bounce at all. It's quite a sight to behold! A simple model can be set up a follows.
We can write with Conservation of Energy (the collision is clearly not elastic - as evidenced by the permanent deformation of the bottom of the cup):
$$(M+m)gH=mgh+W+\Delta Q+K_{M+m}$$
where:
Trouble is, we don't know the value of $W+\Delta Q+K_{M+m}$. Direct observation suggests it is small, so we can write:
$$(M+m)gH\geq mgh$$
Or:
$$\boxed{h \leq H\Big(\frac{M+m}{m}\Big)}$$
If $M\gg m$ we can further approximate:
$$h \leq \frac{M}{m}H$$
I wanted to confirm experimentally the effect of $M$ on $h$.
Using a nearly empty cup, one half-filled and one filled completely I can confirm increased $M$ increases $h$.
Some further experiments are planned.
As mentioned in the comments above, the ball in the cup is similar to Galilean Cannon. The maximum height to which the ball can bounce $h_{max}$ can be estimated using the law of energy conservation: $$(m+M)gH=mgh+E_{cup}+E_{water}+E_{heat},$$ where $m$ is the mass of the ball, $M$ is the mass of cup+water, $H$ is the initial height from which the ball was thrown, $E_{cup}$, $E_{water}$ and $E_{heat}$ are the energy of cup, water and heat (due to dissipation). The maximum height corresponds to $E_{cup}=E_{water}=E_{heat}=0$. $$h_{max}=\frac{m+M}{m}H$$
As compared to the result by @Gert, for $M\gg m$, $h_{max}$ is proportional to $M$ not $M^2$. The latter would contradict the conservation of energy.
Recall that if a ball normally hits a wall elastically, its velocity will be exactly reversed.
Suppose the whole system hits the ground with speed $v$. Now, as the cup and the water hits the soft mat, their speed quickly reduces, and may start moving upward (depending on how soft the mat is) before the ping-pong ball is affected by a reaction force. Suppose the speed of the cup (and the bottom part of water) becomes $u$, along the upwards direction.
Let's go to the cups frame. Now the ball (and the top level of water) is hitting it with speed $u + v$. If the cup were much (actually infinitely) heavier than the ball, the ball would rebound at speed $u + v$ in this frame (the cup acts like a wall). Since the cup itself was moving upward at speed $u$, the upward velocity of the ball in ground frame will be $2 u + v$.
Now in the actual experiment, the collisions are not elastic, the cup's velocity does not change instantaneously, and the cup is not so heavy compared to the ball. So the final upward velocity of the ball be less than $2u + v$, but the above argument shows why it is greater than $v$.
Why Energy Conservation still holds: Since the cup and most of the water does not bounce back to their initial position, their initial potential energy is available to be converted into the extra kinetic energy of the ball, and the energy absorbed by the mat and water.
As mentioned in the comments, this is similar to a Galilean cannon.
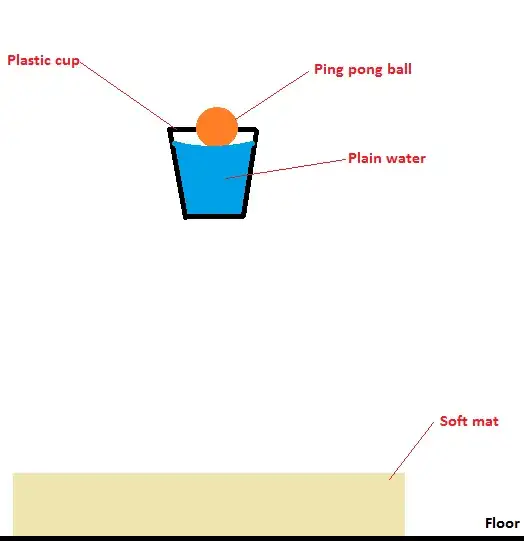
My hypothesis why the ping pong ball receives a large upward impulse:
The floating ping pong ball is displacing some water. The amount of displacement does not change much during the fall.
As the cup hits the floor the deceleration of the quantity of water gives a short pressure peak. Because of that pressure peak the water that is in contact with the ping pong ball is (briefly) exerting a much stronger force upon the ping pong ball. The water reflows, moving down along the walls of the cup, and moving up along the central axis. Thus the ping pong ball receives a large impulse.
It may even be that there is a secondary effect. It may be that the peak in the force exerted on the wall of the cup causes elastic deformation of the cup wall, and as the cup wall bounces back all of that motion focusses on the central axis of the cup, which is right where the ping pong ball is located.
It may well be that after kicking up the ping pong ball the water is left with little energy, so it remains in the cup. My guess is that without the ping pong ball the water will predominantly jump up along the central axis.
This suggests a comparison experiment.
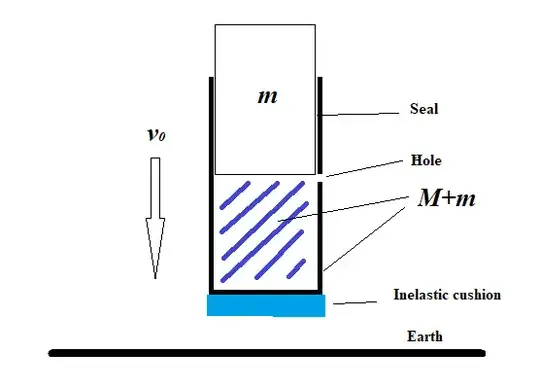
This suggested setup will require some manufacturing. Instead of a cup (which is tapered) a cylinder must be used, and instead of a ball a second cylinder must be used (short, closed at both ends), this second cylinder must slide freely inside the first cilinder. I will refer to these two as 'the cylinder' and 'the piston'. (Of course the cylinder, like the cup, must be closed at one end)
Before release water should not be allowed to enter the gap between piston and the cylinder. (During the fall both will be weightless; not much water will penetrate the gap.)
Under those circumstances I don't expect the piston to bounce up, certainly not higher than the height of release.
The piston is flat underneath, so there is no opportunity for the water to reflow. I think it is the forced reflow that transmits the impulse to the ping pong ball, so I expect that when reflow is eliminated then the ooportunity for impulse transfer is removed.
In a comment and in an anwser it has been suggested that there is a similarity with the a Galilean cannon setup.
However, in the setup of this question the impulse is transferred to the ball by a fluid, which is incompressible. For comparison, imagine trying a Galilean cannon setup where both of the two balls are filled with water. That would not work, because the elasticity of the air in the balls is a crucial element. So, while there is some similarity, the differences are such that comparison with a Galilean cannon setup is not particularly helpful.
Assume that the water in the cup is compressible and inviscid, experiencing one-dimensional flow and thereby satisfying the one-dimensional Euler equations. Initial conditions, velocity =$\sqrt{gh}$ downward and pressure =1 atm, are both uniform. The bottom of the cup is struck from below in such a way that the velocity of the water is reduced and the pressure is increased, similarly to the well-known piston problem. This creates an upward-moving pressure wave inside the water, and produces a pressure gradient in the vertical direction. The pressure gradient creates an upward force on the PPB, instantaneously equal to the submerged volume times the magnitude of the gradient (Archimedes principle). This gives the PPB an initial acceleration, but only for a short period until the PPB leaves the water.
I believe that this has all the makings of a good explanation. but it is terribly hard to put numbers to. Even the decision to include compressibilty needs more justification than I have been able to muster. However, there are times when water at fairly low speeds must be considered compressible. An example is "water hammer" the noise made sometimes by domestic water pipes in response to the sudden closing of a tap. The speeds and decelerations involved might be quite similar.
This is a reaction to the otherwise fine answer of 'Cleonis'.
Here's is his set-up, as I understand it:
The ensemble of cylinder, water and piston hits the Earth at $v_0$ because:
$$\frac12 v_0^2=gH$$
where $H$ is the drop height.
Due to the soft, inelastic cushion at the bottom of the cylinder, the restitution coefficient is $\text{zero}$ and the energy balance is:
$$(M+m)gH=mgh+\Sigma E$$
where $\Sigma E$ are various small energies described in my first post.
In the limit for $\Sigma E \to 0$, we get:
$$(M+m)H=mh$$
Note that a hole in the cylinder is needed as otherwise a partial vacuum between the 'escaping' cylinder and piston would arise.
Under those circumstances I don't expect the piston to bounce up, certainly not higher than the height of release.
So I believe this to be wrong.