Identifying parallel and series capacitors for capacitor system with dieletric inserted

Question

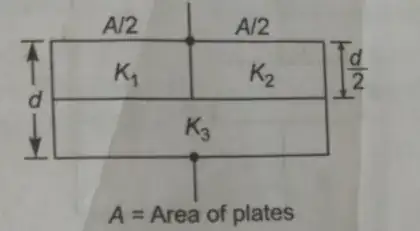
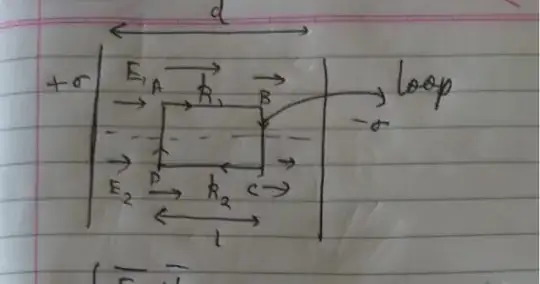
(Source:- JEE 2000).

What I did was prove that the electric fields in K1 and K2 are having the same E fields inside them(as shown in the image ). I then concluded that since the fields are uniform, constant and the distance which the dielectrics k1 and k2 occupies are the same, the potential drop across them should be the same. Related

$$ \oint \vec{E} \cdot dl = 0$$

$$ \implies \vec{E_1} = \vec{E_2}$$

I hence concluded that Slabs k1 and k2 are in parallel and their equivalent would be in series with slab k3 and got the following answer (which is incorrect acc. soltn key).

$$k_{eff} = \frac{2(k_1 +k_2)k_3}{2k_3 + k_1 + k_2}$$

The correct answer given is obtained when we take the slabs k1 and k2 each to be in series with half of k3 each and then taken in parallel.

$$C_{eq} = \frac{\epsilon_oA}{d} ( \frac{k_1k_3}{k_1 +k_3} + \frac{k_2 k_3}{k_2 + k_3})$$

Concerns:-

1. If the voltage differences across the slabs k1 and k2 are equal why are they in series with k3 and not in parallel with each other?
2. On top of this, the capacitors in series have the same charges on them which doesn't seem to be the case here as $Q_{ind}$= $Q(1-\frac{1}{k})$ and since k is different, the charges on all the slabs are different. One of my friends responded to this by stating that capacitors in series need not always have the same charge and gave an example of two capacitors connected by an inductor.

Answer 1

But what's wrong with first taking them in parallel and then series

Let the three capacitances in your proposed connection be $C_1$, $C_2$, and $2C_3$. The equivalent capacitance is then

$$C = 2\frac{(C_1 + C_2)C_3}{C_1 + C_2 + 2C_3} $$

Now, think about what happens when, say, $k_1$ is made much, much greater than $k_2$ and $k_3$. The equivalent capacitance would go to

$$C\rightarrow 2\frac{C_1C_3}{C_1} = 2C_3 = 2\frac{\epsilon_0k_3A}{d}$$

This doesn't pass the sanity check. It doesn't seem plausible that making $k_1$ arbitrarily large should negate the effect of the $k_2$ slab entirely.

The equivalent capacitance of the correct parallel combination of two series connected capacitors is

$$C = \frac{C_1C_3}{C_1 + C_3}+\frac{C_2C_3}{C_2 + C_3}$$

and the limit of arbitrarily large $k_1$ is

$$C\rightarrow C_3 + \frac{C_2C_3}{C_2 + C_3} \lt 2C_3$$

This does pass the sanity check. Only if $k_2$ is also made arbitrarily large does the equivalent capacitance approach $2C_3$.

So where has your thinking gone wrong? If the connection you propose is valid, then we can insert an ideal conductor plate at the interface of the $k_3$ dielectric with the others without changing the system. But I'm almost certain that's not the case.

With the plate there, the electric field lines must be 'vertical' (normal to the plate) at the interface. But, without the plate there, I don't believe that there's a requirement that the field lines are normal to the dielectric interfaces.