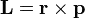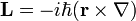A universe of angular momentum?

Question

I read this on Wikipedia:

[...] That most tangible way of expressing the essence of quantum mechanics is that we live in a universe of quantized angular momentum and the Planck constant is the quantum. [...]

And I'm wondering if anyone can explain this a little more. Is it saying that ALL action is made up of angular momentum which is quantised in units of Planck's constant? Or is it just saying that all matter is composed of particles which have quantised angular momentum?

If the answer is the prior, this would mean that a photon's movement through space is as a result of angular momentum, which seems strange.

Anyway, if you could help me out with a little explanation, that would be great.

Answer 1

This is a comment turned into an answer.

Classically one can define an angular momentum of a straight track with respect to any axis as

The real meaning though comes from rotational states about a central axis. In this case a potential exists which constrains the particle to revolve about the axis.

Quantum mechanically one defines an angular momentum in potential problems where there exists a solution as a wave function and the corresponding angular momentum operator acts on these functions:

The result of this action will display the quantization of angular momentum, the value being a multiple of h_bar as shown in the table of the link.

The not very clear argument you are quoting from the wiki article is based on the assumption that quantum mechanically there will be an angular momentum only if a potential exists binding a particle, which will then inevitably have a quantized angular momentum. In the microcosm there cannot be a rotation about a center without a potential problem so it is true, but not, in my opinion the easiest way to understand quantum mechancis !.

Answer 2

The Wikipedia page has been modified since the question was posed and the cited text disappeared, which is a good thing as it does not make much sense. Now it can be interesting to note that the preceding sentence was

Action is a general physical concept related to dynamics and is most easily recognized in the form of angular momentum.

So I take it that the original wiki editor had in mind the path integral formulation where the action (a quantity with the same units as angular momentum, and the Planck constant) is responsible for the phase relationship between alternate paths and thus governs their interference.

From this perspective the action could maybe be argued to represent the essence of quantum mechanics. But it would be very misleading to formulate this idea by confusing action and angular momentum; see this post for a related discussion.

Answer 3

Over the decades generations of teachers have attempted to come up with an intuitive way of introducing quantum mechanics, and all have failed since it's fundamentally non-intuitive. These days students are usually just presented with the Schrödinger equation and told to get on with it. By solving the Schrödinger equation you are deriving energy eigenfunctions, so your starting point would be that the basis of QM is that energy is quantised (well, for most bound systems anyway).

The Wikipedia article is attempting to introduce QM as quantised angular momentum. I don't know if this is technically possible, though I would have guessed not since I can't see how you'd derive the radial part of the hydrogen wavefunction without considering energy. Whether it's technically possible or not, it seems to me to be unhelpful and confusing for students new to QM. I would ignore that article and find some other better introduction.

A formal introduction would probably start from the axioms of quantum mechanics, though these are far from intuitive. The Schrödinger equation follows from the axiom that time evolution acts linearly on states.