0

So I was looking at this post and I started thinking about this.

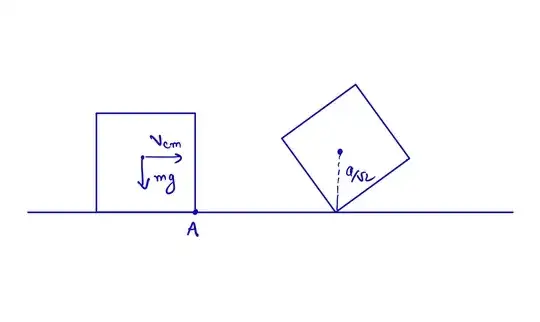
Let's say I have a cube-like object on the floor. Friction is not zero. Suddenly, I apply a momentary force at a place that will create torque. Consider this diagram:

enter image description here

Given enough momentum/force/torque, is it possible that the square will gain height such that it will stop touching the ground? If so, which is the last point that will touch the ground? Maybe the bottom right corner(edge)?

My thoughts: I think it will takeoff. Because if not, it would have to keep doing the weird square spin at high velocity...this is not realistic. I guess the vertical acceleration caused by both the bullet and the ground can be high enough? I also guess a minimum torque will be needed, else the object would just slide....

George Menoutis
  • 430

1 Answers1

0

enter image description here

The figure shows that you would require to rotate the cube at least till highest point to tip it off. So assume that after collision the acquire $\omega$ as angular speed such that $\omega=\frac{v_{cm}}{a/2}$. So using energy conservation $$\frac{1}{2}I\omega^2=Mg(\frac{a}{\sqrt{2}}-\frac{a}{2})$$ where $I$ is the moment of inertia about the edge. So $I=\frac{ma^2}{6}+m(\frac{a}{\sqrt{2}})^2=\frac{2Ma^2}{3}$. So minimum $V_{cm}$ required is, $$\frac{2Ma^2}{2*3}\frac{4v_{cm}^2}{a^2}=Mga(\frac{1}{\sqrt{2}}-\frac{1}{2})$$ $$v_{cm}=\frac{\sqrt{3ga(\frac{1}{\sqrt{2}}-\frac{1}{2})}}{4}$$ Now use conservation of momentum and conservation of energy to calculate the momentum required by bullet to tip it off, $$\frac{1}{2}mv_1^2=\frac{1}{2}I\omega^2$$ $$mv_1=Mv_{cm}+mv_2$$ where $v_1$ and $v_2$ are the final velocity of the bullet.

sslucifer
  • 1,017