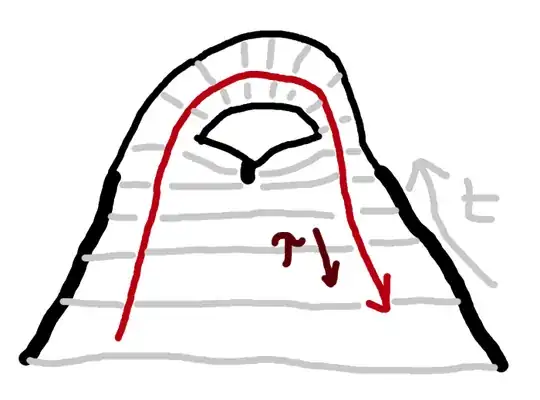
On a surface embedded in Euclidian space, where the metric signature is all positive, it is possible for a particle traveling along a geodesic to encounter a curved bit and then get turned around so that it heads in the opposite direction (so that an increase in the parameter of the curve leads to a change in the coordinate in the opposite direction as before).
Could there be a manifold that did the same turning-around trick, but in a timelike direction? Would this create particles for which increasing proper time corresponded to decreasing coordinate time?
How this idea is distinct from closed timelike curves
Oddly, last time I asked this question, it was closed as a duplicate of this other question: What would a closed timelike curve look like? This is unfortunate because it had a very good answer from yukterez that I was planning to accept! So here is an explanation of how I am not asking about closed timelike curves:
1. A patch of spacetime that turns worldlines around would not always create closed curves.
A closed timelike curve must be, well, closed. If an object were to enter in to a part of spacetime like I am describing, it could exit at a different point in space and head backwards through time (with respect to its proper time) in such a way that it did not return to its starting point. Therefore the set of things I am talking about is not a subset of all closed timelike curves.
2. Closed timelike curves do not always involve coordinate time moving opposite to proper time.
A simple example of a geometry leading to closed timelike curves would be the torus. An object heading in to the future would always show up back in the past. However, for any natural time coordinates this would not reverse the direction of proper time with respect to coordinate time. At any point along the worldline of the object, advancing proper time would correspond to advancing coordinate time. This would not be the case for what I am talking about! Therefore, the set of closed timelike curves is not a subset of what I am talking about.
Conclusion
Since CTCs are neither a superset nor a subset of what I am talking about, I think we must all agree that this is not a question about closed timelike curves per se.
Illustration
Here is a depiction of a geodesic like what I'm imaging. Please forgive any inaccuracies, I am not a good artist! (I meant to draw the ribbon twisting so that it would actually be a geodesic in Euclidian space but it didn't come out right.) This is mainly intended to be interpreted strictly by a definition: proper time and coordinate time align for a while, then the geodesic turns around and they go opposite.