What happens to the magnetic field in this case?

Question

As far as I know, it's possible to create a radially polarised ring magnet, where one pole is on the inside, and the field lines cross the circumference at right angles.

So imagine if I made one which was shaped like a sector of a torus.

Then I forced a load of these magnets into a complete torus.

Clearly this magnet is impossible because there's no way for the field lines to get back into the middle. So what happens to the field in this case? Does it disappear completely? Do the magnets blow up?

Answer 1

The field would disappear completely.

I think the simplest explanation is in terms of the surface currents that account for the field (assuming constant magnetization, which is reasonable for thin slices). For the initial torus magnet (your second image) the magnetic field is generated, in practice, by surface currents on the planar ends of the torus. One runs clockwise as seen on the image - the one nearest the viewer - while the rear planar face has an anticlockwise current on it.

If you now stack two of those together, the surface currents on the faces in contact will cancel out, giving a bigger version of the same thing. The field will then be created just by the surface currents at the ends of the tube.

You then propose adding more magnets in this fashion until the ring is closed. That will bring the two remaining planar surfaces with surface currents into contact, cancelling out those currents. The resulting magnet will have zero surface current and therefore zero magnetic field.

Answer 2

I think Emilio Pisanty's answer is good enough. But here is another longer, 'magnetic charge' approach. (

Let's specify the coordinates first (sorry I borrow your picture).

It's obvious that the toroid is symmetrical under rotation along $\hat{\phi}$ direction. Thus we can't have magnetic field along $\hat{\phi}$. Which means it is sufficient for us to find the magnetic field on the $xz$ plane, and we can generalize later by rotating this $xz$ plane.

We have some constrains to consider here due to the shape of torus:

• $\vec{B}$ is symmetrical under reflection over $\hat{x}$ axis and $\hat{z}$ axis.

• $\nabla\times B=0$.

• $\nabla.B=0$

The most general field lines in $xz$ plane that satisfy these conditions roughly looks like this.

Now we only have two possible directions, the one shown in the picture or the opposite of that(or zero everywhere). We can apply magnetic Gauss law here with the Gaussian surface marked with black dotted line(in 3D point of view this black dotted line is rotated along $\phi$ so that the product looks like a mountain).

The only part of the Gaussian surface which has magnetic flux through it is the top part. The remaining area is intentionally shaped to follow the field lines tangentially so that there's no flux through it. Now we only need to determine whether the magnetic charge inside the envelope is positive or negative(Positive charges are shown in blue, and negative charges in red). As we can see in the picture, the inner magnetic field which is represented by yellow lines may bend slightly from radial direction towards the direction which allows the envelope to catch more or less positive charge. So the total charge inside the envelope might be positive or negative. However if the yellow lines bend in a way like that, then we will meet a kink somewhere between the inner and outer field or we may also get a non-zero curl field and these are impossible. So we are only left with a radial inner field. And therefore the total charge inside the envelope is zero and there can't be any flux passing through it. So in conclusion the field outside must vanish everywhere.

Answer 3

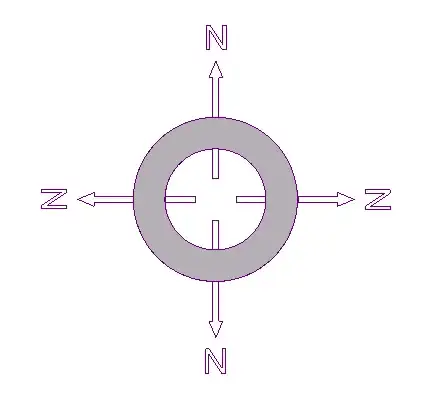
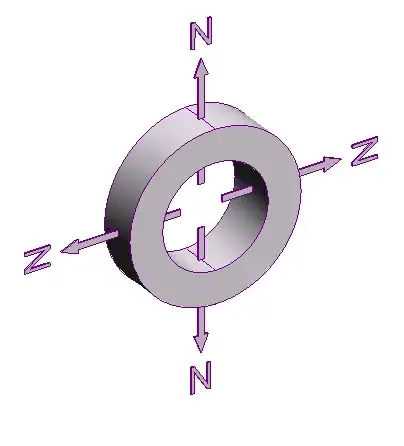
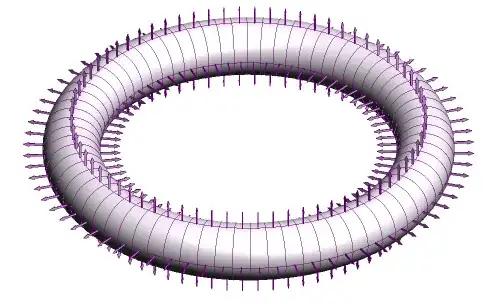
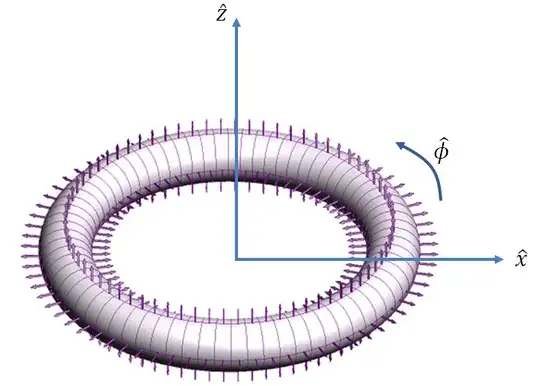
I am writing a new answer so that psx community can judge my idea regarding the energy issue independently.

The work done in order to assemble the pieces together will simply be converted to the magnetic potential energy of the system. When the pieces are put together, the system will have a tendency to blow apart without involving any singularity and demagnetization is unnecessary(the magnetic field outside the "meat" will decreases as more pieces are put together). Even though the magnetic field vanishes everywhere except in the "meat", it does not mean that there is no magnetic potential energy.

The total magnetic field in all space says nothing about the amount of extractable potential energy of the system. Mathematically the total magnetic field energy of a system is

$E=\frac{μ_0}{2} \int B_{tot}^2 dV$

Where $B_{tot}=Σ B_i$ , $B_i$ is the magnetic field due to a small portion of magnet.

However not all of this energy is extractable, the extractable potential energy of the system is the negative* of sum of the cross terms

$U=-\frac{μ_0}{2} \int (Σ_{i≠j} B_i B_j) dV$

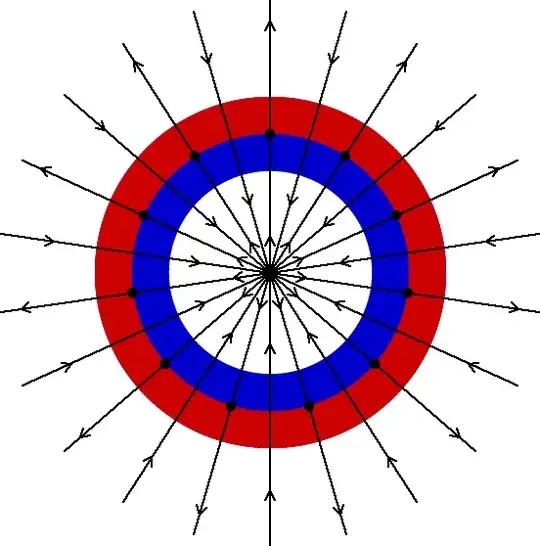
We know that it is mathematically possible to have $B_{tot}=0$ everywhere while having $Σ_{i≠j} B_i B_j\neq0$. So it is possible that $U\neq0$ in such case, which removes the paradox.

We can also write the magnetic potential energy in terms of magnetic moments

$U=-∫\vec{B_{ext}} . \vec{dm}$

Where $\vec {dm}$ is infinitesimal magnetic dipole element, and $\vec{B_{ext}}$ is the total magnetic field at the dipole excluding the magnetic field due the dipole itself.

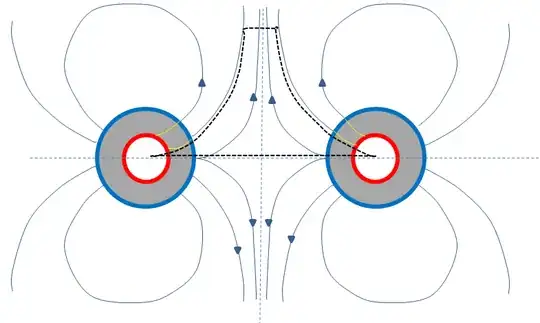
Though we assume that the magnetization is permanent, meaning that $\vec{dm}$ is unchanged, there is nothing that prevents $\vec{B_{ext}}$ from changing. If we draw the field lines, we can see that it is more likely that $\vec{B_{ext}}$ on a single piece of magnetic dipole increases as more and more segments are put together. We can also see that $\vec{B_{ext}}$ tends to be anti-parallel to $\vec {dm}$. Therefore the total potential energy will be positive and its value increases as more and more pieces are put together. Which suggests that the segments tend to blow apart when put together. Due to the geometry of the system it is hard to give a rigorous proofs of my last few statements. However, no matter how complicated the system is, we can still be sure that there are many rooms for the energy to hide. Thus the conservation of energy is still safe.

---

*Note that the negative sign here is not obvious. In the case of electric charges we would pick the positive of the sum, instead of its negative. The explanation of the sign can be found in my blog http://wp.me/p1AI8o-2P; It is also explained briefly in Feynman Lectures on Physics Vol.2 ch.15.

Answer 4

An object becomes magnetized not only by aligning all relevant molecules into a lattice-type structure, but also by flipping what are called molecular domains. These larger level magnetic regions must also be aligned, usually in rapid succession, during the application of high electric current in the magnetizing process. Aligning the North rings side by side will become increasingly difficult as anyone who has tried to manually build a Halbach Array knows. Assuming that the final piece is in place, (and this requires an external frame), the magnetic field will only be zero theoretically because that assumes a perfectly structured lattice at the molecular level and it assumes that the larger magnetic domains will not flip under the strain. The real world imperfections will find the system's weak spots and create holes in which South will flow through, much like Swiss cheese. This principle is also evident on large surface disk magnets, neodymium included, as their Gauss readings are not uniform and show substantial variation. In some cases, if the molecular lattice is weak enough, physical chunks of magnetic material will blow off, adding to the holes. In summary, trying to physically shut down a magnetic field of an object at the macro level is not the same as uniformly demagnetizing that object at the microscopic level. -- James R. Williamson, Jr.

Answer 5

I come to the same conclusion as Emilio Pisanty directly, but by using superposition.

A simpler model with the same features as the toroidal one is to assemble prismoidal magnets to form a sphere, say with the North poles outside and the South poles inside. Even simpler, work in a lower dimension, in a plane, and assemble trapezoidal magnets in a circle, again, oriented with the same pole outside.

The following picture represents the magnet, and the field lines. A dot marks the origin of each field line.

Then, by superposition, the magnetic field cancels itself. One way to think about this is that, because of the spherical symmetry, the field is identical to a spherical field sourced in the center, so that the North and South poles coincide.

Peter Shore asked about energy conservation. I guess a lot of energy is needed to assemble together the magnets, and it can be recovered if we let the magnets forming the sphere free, since they continue to repel each other.

Answer 6

My intuition tells me that if the radius of the ring is large enough, a radial magnetic field should be possible. A ring having a small radius would cause a cancellation of the field. Say for example the ring was 10 ft in diameter. Surely such a diameter would permit a radial field. Magnetic fields will only cancel each other if they are sufficiently close to each other.

A sphere on the other hand is a bit of a weird case. since there is no "escape" for the internal pole, it would seem logical to say there would be perfect cancellation of the field. Unless nodes form creating a field that varies at regular intervals.

I don't see why a spherically radial field wouldn't be possible if the magnets aroung the sphere were evenly spaced.

Answer 7

If all of the segments necessary to form such a toroid could be put in place, it would form a larger, and more powerful, version of one of the segments except that it would be hollow instead of solid. This is possible due to the fact that a magnetic field is capable of penetrating, and passing through, the material of which the segments are made, and also of realigning the particles/atoms of the material. The field, and the alignment of particles/atoms in the material, would simply shift in order to acheive a field as uniformly balanced as possible (one with as close to uniform field pressure as possible).