The common bar magnet has the north pole on one end and the south pole on the other. I was wondering if we cut the magnet into the following shape (a part of a thick spherical shell)
And then assuming we could arrange several of these into a sphere, gluing them together using some super strong glue or soldering them:
Would this be, in effect, a "magnetic monopole"?
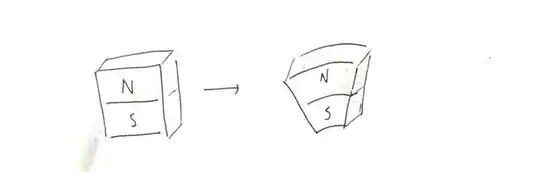
No. Outside the sphere, the magnetic field due to the outer "north" shell is exactly canceled by the magnetic field due to the inner "south" shell, and so $\vec{B}=0$ outside the shell. This is easier to see if you think of it in analogy to a spherical shell carrying a positive charge on the outer surface and a margarine charge on the inner surface; if the electric charge on the two surfaces are equal, then there is no field in the exterior.
More rigorously, we can imagine a thick shell with a purely radial magnetization $\vec{M}$. Since the curl of this vector field is zero, there is no bound current in the bulk of the sphere; and since the surfaces are orthogonal to the magnetization, there are no bound surface currents. In other words, there are no currents anywhere and so the magnetic field vanishes everywhere -- including, surprisingly, in the bulk of the magnetized shell.
