When a photon hits a half-silvered, mirror quantum mechanics says that rather than being reflected OR transmitted it enters into a superposition of transmitted AND reflected (until a measurement takes place). Is there an experiment that demonstrates that this is actually the case and that the photon didn't end up with a single outcome all along? In other words, is the superposition view just a hypothesis that can't be proven either way?
3 Answers
There is a very nice experiment that does this for 2 photons: it is the Hong-Ou-Mandel experiment:
C. K. Hong; Z. Y. Ou & L. Mandel (1987). "Measurement of subpicosecond time intervals between two photons by interference". Phys. Rev. Lett. 59 (18): 2044–2046.
For simplicity, consider two photons simultaneously entering a beam splitter described by the unitary matrix
\begin{align}
U=\left(\begin{array}{cc} U_{11}&U_{12} \\ U_{21}&U_{22}\end{array}\right)\, .
\end{align}
Each photon of the two-photon input state $a_1^\dagger a_2^\dagger \vert 0\rangle$ is then scattered into a superposition
\begin{align}
a_1^\dagger &\to a^\dagger_1 U_{11} + a^\dagger_2 U_{21}\, ,\\
a_2^\dagger &\to a^\dagger_1 U_{12} + a^\dagger_2 U_{22}\,
\end{align}
so the output state is a product of superpositions:
\begin{align}
\left(a^\dagger_1 U_{11} + a^\dagger_2 U_{21}\right)
\left(a^\dagger_1 U_{12} + a^\dagger_2 U_{22}\right)\vert 0\rangle\, .
\tag{1}
\end{align}
The experiment then measures the rate at which photons are counted in different detectors, i.e. it excludes from the total amplitude (1) terms in $a^\dagger_1a^\dagger_1$ and $a^\dagger_2a^\dagger_2$. This is illustrated as follows:
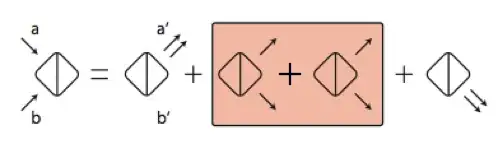
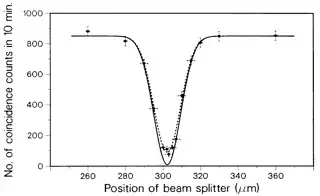
The count rate is then proportional to \begin{align} \vert U_{11}U_{22}+U_{12}U_{21}\vert^2\, , \tag{2} \end{align} and thus detects the interference between the path. A model where the photons would not output in a superposition would not have a sum of products of terms.
In the original experiment, HOM used a $50/50$ beam splitter and the relative phase upon reflection leads to $\vert U_{11}U_{22}+U_{12}U_{21}\vert^2=0$: basically the path destructively interfere. HOM also controlled a relative time delay between the photon pulse by adjusting the position of the beamsplitter in their setup, and the 0-rate only occurs when the pulses perfectly overlap so the photons are exactly indistinguishable.
You can find more details with full time delays and various pulse shapes in this paper:
Brańczyk, Agata M. "Hong-ou-mandel interference." arXiv preprint arXiv:1711.00080 (2017).
The quantity $U_{11}U_{22}+U_{12}U_{21}$ is actually the permanent of the scattering matrix $U$. It need not be $0$ in general but happens to be $0$ for the $50/50$ beam splitter. The notion of permanent is defined for an $n\times n$ matrix, and is at the core of the BosonSampling proposal to show how a (single purpose) quantum computer could outperform a classical computer.
As additional material prompted by comments:
Assuming for simplicity Gaussian pulses of unit width with maxima separated in time by $\tau$, the rate is given by \begin{align} \textstyle\frac{1}{2}(1+e^{-\tau^2})\vert U_{11}U_{22}+U_{12}U_{21}\vert^2 +\textstyle\frac{1}{2}(1-e^{-\tau^2})\vert U_{11}U_{22}-U_{12}U_{21}\vert^2\, . \end{align} Thus, for exact overlap, $\tau=0$ and only the first term remains. In a 50/50 beam splitter the combination $U_{11}U_{22}+U_{12}U_{21}=0$ so the rate is exactly $0$.
For partial overlap and a 50/50 beam splitter, one is left with the second term, which contains the determinant of the scattering matrix. If the scattering matrix is unitary, this determinant is of magnitude 1 so the rate is basically given by $\sim (1-e^{-\tau^2})$, going smoothly to $0$ as $\tau\to 0$.
- 49,168
- 21
- 71
- 148
When the photon is detected, it always ends up with a single outcome. The superposition is simply an expression of the fact that until it is detected there are non-zero probabilities for different outcomes.
Confusion arises because there is a fundamental difference between probabilities given in quantum mechanics and classical probabilities. In classical probability theory outcomes are determined by unknowns, but quantum mechanics describes situations in which outcomes are actually indeterminate. This naturally alters the way in which probabilities are calculated.
Textbooks, and physicists generally, are usually concerned with applications, and in doing the calculations, not the underlying mathematical reasons why we calculate probability in quantum mechanics in the way in which we do, but it is known in the mathematical foundations of quantum mechanics that the general form of the Schrodinger equation is required by the probability interpretation, and that consequently we calculate using wave mechanics.
- 11,871
The photon is observed in one of the two states with some probabilities, the superposition itself is not observable (you may have heard of the Schrödinger cat – an analogy that was used about a hundred years ago to pose the same question that you are posing now).
The superposition can however be tested in interference experiments, studying diffraction patterns etc. Otherwise, indeed, it would be indistinguishable from simply being reflected/transmitted with a given probability, which would make the quantum mechanics unnecessary.