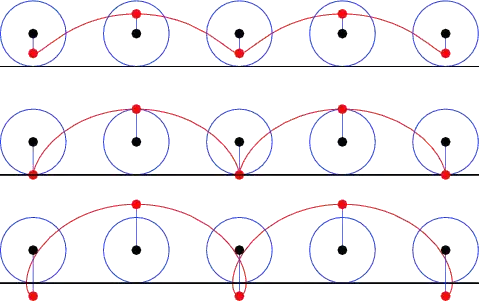
Cycloid is a type of trajectory which is traced by a point on the circumference of a planar circle rolling without slipping on a surface. It turns out that this is the solution to the Brachistochrone problem, that is the curve along which a material particle may slide without friction in the least time, under the acceleration due to gravity or any uniform force field (such as a charged particle in an electric field). Besides, the path that light takes through an optically non-homogeneous medium is also a cycloid. This intriguing connection of the resulting trajectory being the same for these phenomena has been explored and is explained beautifully by Steven Strogatz in this video.
However, the motion of a charged particle in a uniform crossed electro-magnetic (EM) field is also a cycloid. Is there an intuitive explanation (perhaps from a Hamiltonian perspective) why this correspondence exists? It is tempting to guess the Hamiltonian perspective to explain this equivalence of the resulting dynamics since all these phenomena must follow from minimizing an action. Additionally, please feel free to contribute any ideas or cite any references addressing any relationship with the Fermat's principle of least action of light (cycloid in non-homogeneous medium) which in effect is also a crossed EM field and the trajectory of a charged particle in a uniform crossed EM field?