I'm trying to solve a homework problem. The statement of the problem says:
"When the negatively charged plate of a parallel plate capacitor is lit up by light of a certain wavelength, electrons are emitted from it with velocities in random directions (Photoelectric effect). Show what values can the magnitude of an applied constant magnetic field take such that it is guaranteed that no emitted electron reaches the opposite plate".
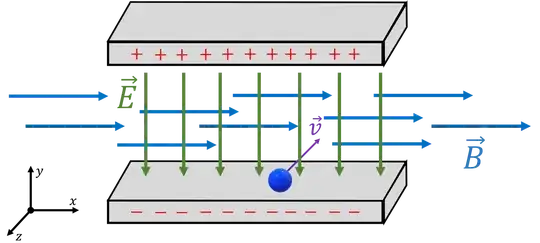
I made the following diagram showing the elements at play in this problem.
The way I approached a solution for this was to try and find the equation of motion for the electron.
We know that the Lorentz force states: $$ \vec{F} = q(\vec{E} + \vec{v} \times \vec{B}) $$ Using the problem statement and the reference system in the diagram, we have that $\vec{E} = E(\mathbf{-\hat{j}})$, $\vec{B} = B\mathbf{\hat{i}}$. Also, since $\vec{v}$ is in an arbitrary direction we can say that $\vec{v} = (v_x,v_y,v_z)$. Using Newton's second law we can put all of this together:
$$ m \begin{pmatrix} \dot{v_x} \\ \dot{v_y}\\ \dot{v_z} \end{pmatrix} = q \begin{pmatrix} \begin{pmatrix} 0 \\ -E\\ 0 \end{pmatrix} + \begin{pmatrix} v_x \\ v_y\\ v_z \end{pmatrix} \times \begin{pmatrix} B \\ 0\\ 0 \end{pmatrix} \end{pmatrix} $$ which after simplifying leads to: $$ \begin{pmatrix} m\dot{v_x} \\ m\dot{v_y} \\m\dot{v_z} \end{pmatrix} = \begin{pmatrix} 0 \\ q(Bv_z -E) \\-qBv_y \end{pmatrix} $$ From here we can establish a system of equations. Since we're interested in how high the electron goes ($y$-direction) we can establish a differential equation involving only $v_y$ and solve from there. We see that: $$ v_z = \frac{m\dot{v_y}}{Bq} +\frac{E}{B} $$ substituting this in $\dot{v_z}$ we get: $$ m \frac{d}{dt}\left(\frac{m\dot{v_y}}{Bq} +\frac{E}{B}\right) = -qBv_y $$ Since we're assuming that $\vec{B}$ is constant and we know that in a parallel plate capacitor $\vec{E} = \frac{\sigma}{\epsilon}$ is independent from time, we get: $$ \frac{m^2\ddot{v_y}}{Bq} = -qBv_y $$ $$ \implies \ddot{v_y} = -\left(\frac{Bq}{m}\right)^2 v_y $$ Since this is a second-order linear ordinary differential equation, we have that the general solution for this is given by: $$ v_y(t) = c_1 \cos\left(\frac{Bq}{m}t\right) + c_2 \sin\left(\frac{Bq}{m}t\right) $$ From here we can say that $v_y(t=0) = v_{y_0}$ for some initial velocity. Which means that $c_1 =v_{y_0}$. If we integrate $v_y(t)$ with respect to time we get the equation of motion in the $y$ direction: \begin{align} y(t) &= \int_{0}^{t} v_{y_0} \cos\left(\frac{Bq}{m}\tau \right) + c_2 \sin\left(\frac{Bq}{m}\tau\right) \ d\tau\\ &=\left(\frac{m}{Bq}\right)\left(v_{y_0} \sin\left(\frac{Bq}{m}t \right) - c_2 \left[\cos\left(\frac{Bq}{m}t\right) -1\right]\right) \end{align}
And here's where I got stuck. I tried using the initial condition that $y(t=0) = y_0$ to solve for $c_2$, but if I plug in 0 everything in the expression goes to regardless of the value of the constant, making me unable to solve for $c_2$.
The second point I don't know how to go about is solving for $B$. I'm not sure if it's possible to solve explicitly for $B$ while having the variable inside trig functions and also multiplying them.
I would appreciate it if someone could help me and tell me if I'm on the right path, and if so, how can I continue from here?