De Broglie waves

Question

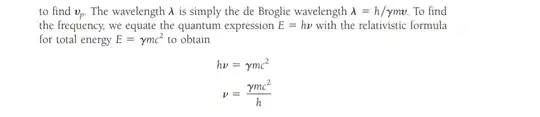
While deriving the expresson for phase velocity in context of de broglie waves, in arthur beiser, book he has equated the quantum expresson $hv$ with relativistic formula, but this is not correct . While the first one is only for photon ( having rest mass zero).

The same has been done in Berkeley quantum physics, and they are saying its assumption. So is this assumption true? Why all the books written same thing? Why can't we do without this absurd assumption? Am I getting wrong somewhere?

1 st pic - beiser 2 - Berkeley

Answer 1

$E=h\nu = hf = \hbar \omega$ is true in general. I don't know why you say it is not correct.

Likewise $p=h/\lambda=\hbar k$ is true in general.

$E=hc/\lambda$ is the tricky one which is only true for $m=0$ photons.

Answer 2

When I conceived the first basic ideas of wave mechanics in 1923–1924, I was guided by the aim to perform a real physical synthesis, valid for all particles, of the coexistence of the wave and of the corpuscular aspects that Einstein had introduced for photons in his theory of light quanta in 1905.

                                                                      -De broglie

So If you are talking about wave nature of a particle (matter waves) then you can localize the particle at some point so can't define energy in term of rest energy and kinetic energy because that represent particle energy.Energy of quanta is equal to $h\nu$ that suggest De broglie may be it's valid for matter waves too.In both picture energy should be same and so relativistic energy of particle must equal to wave energy $$h\nu=\gamma m_0 c^2.$$ So In some sense as when electromagnetic waves are quantized you get photon (particle nature) same is true for matter waves.