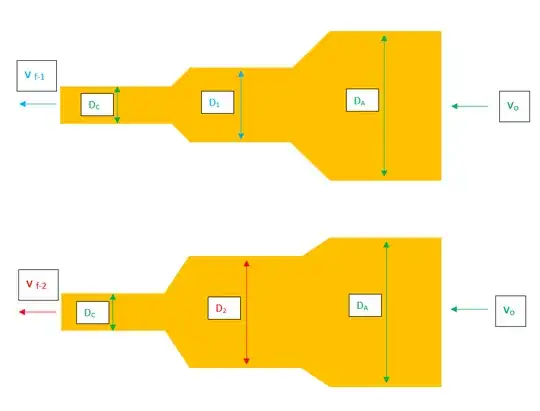
I do not frequently post on this community, so hopefully my question fits within the community guidelines. Below is a picture of two pipe systems. All values that are color coded in green are identical between the two pipe systems (e.g. $v_o$, the inflow velocity, in the upper system is equivalent to $v_o$ in the bottom system).
The primary parameters that I am interested in is how a change in the middle chamber's diameter ultimately affects the final velocity $v_f$ exiting the smallest chamber of the pipe system. For clarification, $D_1 \lt D_2$. I wanted to confirm that, correspondingly, $v_{f-1} \lt v_{f-2}$.
If this is correct, I would greatly appreciate any intuitive idea as to why this is the case. I assume it has something to do with the kinetic energy of fluid molecules in the top system being lower than the kinetic energy of the fluid molecules in the bottom system after transiting through the middle chamber (perhaps as a consequence of experiencing more total resistance during the passage through the pipe system).
In the event that any further assumptions are required to best answer this question, assume the following:
- the length of each chamber is the same between the two systems
- the length of the connecting pieces (i.e. the sloped transition sections) are the same between the two systems. However, these transition sections are obviously increasing their diameter at different rates (but I don't think this really affects the answer)
- gravity is either acting downwards OR right-to-left (but I don't think this really affects the answer)
- the fluid is water (so it can be assumed to be incompressible)
Thank you! Cheers~
The following are orders of magnitude that the parameters referenced in the above picture will tend to float around:
- diameter $\lt 4$mm
- pressure $\lt 80$ mmHg
- velocity $\lt 20$ cm/sec
- Re $\lt 20$