What is (meant by) a non-compact $U(1)$ Lie group?

Question

In John Preskill's review of monopoles he states on p. 471

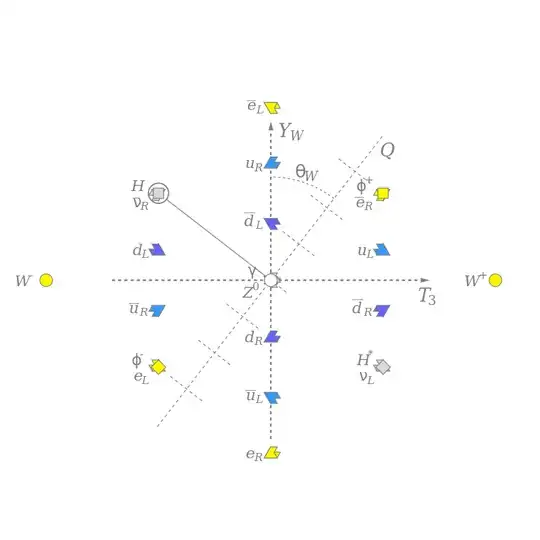
Nowadays, we have another way of understanding why electric charge is quantized. Charge is quantized if the electromagnetic $U(l)_{\rm em}$ gauge group is compact. But $U(l)_{\rm em}$ is automatically compact in a unified gauge theory in which $U(l)_{\rm em}$ is embedded in a nonabelian semisimple group. [Note that the standard Weinberg-Salam-Glashow (35) model is not "unified" according to this criterion.]

The implication of the third sentence is that, in some circumstances, the $U(1)_{\rm em}$ gauge group may not be compact. How could this be? Since $U(1)$ as a differentiable manifold is diffeomorphic to $S^1$ isn't it automatically always compact?

The following paragraph:

In other words, in a unified gauge theory, the electric charge operator obeys nontrivial commutation relations with other operators in the theory. Just as the angular momentum algebra requires the eigenvalues of $J_z$ to be integer multiples of $\frac{\hbar}{2}$, the commutation relations satisfied by the electric charge operator require its eigenvalues to be integer multiples of a fundamental unit. This conclusion holds even if the symmetries generated by the charges that fail to commute with electric charge are spontaneously broken.

is OK, but I don't follow what that has to do with the compactness of $U(1)$.

Answer 1

By the "noncompact $U(1)$ group", we mean a group that is isomorphic to $({\mathbb R},+)$. In other words, the elements of $U(1)$ are formally $\exp(i\phi)$ but the identification $\phi\sim \phi+2\pi k$ isn't imposed. When it's not imposed, it also means that the dual variable ("momentum") to $\phi$, the charge, isn't quantized. One may allow fields with arbitrary continuous charges $Q$ that transform by the factor $\exp(iQ\phi)$.

It's still legitimate to call this a version of a $U(1)$ group because the Lie algebra of the group is still the same, ${\mathfrak u}(1)$.

In the second part of the question, where I am not 100% sure what you don't understand about the quote, you probably want to explain why compactness is related to quantization? It's because the charge $Q$ is what determines how the phase $\phi$ of a complex field is changing under gauge transformations. If we say that the gauge transformation multiplying fields by $\exp(iQ\phi)$ is equivalent for $\phi$ and $\phi+2\pi$, it's equivalent to saying that $Q$ is integer-valued because the identity $\exp(iQ\phi)=\exp(iQ(\phi+2\pi))$ holds iff $Q\in{\mathbb Z}$. It's the same logic as the quantization of momentum on compact spaces or angular momentum from wave functions that depend on the spherical coordinates.

He is explaining that the embedding of the $Q$ into a non-Abelian group pretty much implies that $Q$ is embedded into an $SU(2)$ group inside the non-Abelian group, and then the $Q$ is quantized for the same mathematical reason why $J_z$ is quantized. I would only repeat his explanation because it seems utterly complete and comprehensible to me.

Note that the quantization of $Q$ holds even if the $SU(2)$ is spontaneously broken to a $U(1)$. After all, we see such a thing in the electroweak theory. The group theory still works for the spontaneously broken $SU(2)$ group.

Answer 2

1. Generally speaking, we have$^1$ $$\text{Compact } U(1)~\cong~(e^{i\mathbb{R}}, \cdot)~\cong~S^1,$$ and $$ \text{Non-compact } U(1)~\cong~(\mathbb{R},+).$$

2. E.g. the covering group of the compact $U(1)$ is the non-compact group $(\mathbb{R},+)$.

3. In general, given a gauge theory with gauge group $G$, we can always view it as a gauge theory with gauge group equal to the covering group $\tilde{G}$. (NB: the opposite is not always possible.)

4. E.g. for stand-alone QED with gauge group $U(1)_Q$, then pt. 3 is a not very interesting observation.

5. Let us now return to OP's first quote of Ref. 1. The Glashow-Weinberg-Salam electroweak theory has a non-semisimple gauge group $$G~=~SU(2)_I \times U(1)_Y~\supset~ U(1)_I\times U(1)_Y.$$ Note that the electromagnetic subgroup $H=U(1)_Q$ is regularly/compactly/commensurably/topologically (irregularly/non-compactly/incommensurably/non-topologically) embedded in $G$ if the tangent to the Weinberg angle $\tan\theta_W$ is rational (irrational), respectively, cf. Fig. 1 & 2. This fact is what is behind the first quote in Ref. 1.

$\uparrow$ Fig. 1. (From Wikipedia.) The Cartan subalgebra $u(1)_I\oplus u(1)_Y \subset su(2)_I\oplus u(1)_Y$. The horizontal axis is (the third component) of the weak isospin $I_3=T_3$, and the vertical axis is the weak hypercharge $Y$. The axis of electric charge $Q$ is slanted by the Weinberg angle $\theta_W$.

$\uparrow$ Fig. 2. (From Ref. 2.) The Cartan torus $U(1)_I\times U(1)_Y$ of $G$ is a square with opposite edges identified. An electromagnetic gauge transformation traces out the line $Aaa'bb'cc'dd'ee'\ldots$. If $\tan\theta_W\in \mathbb{R}\backslash\mathbb{Q}$ is irrational, then the electromagnetic subgroup $H=U(1)_Q$ is non-compactly embedded.

References:

1. J. Preskill, Magnetic Monopoles, Ann. Rev. Nucl. Part. Sci. 34 (1984) 461-530; p. 471. The PDF file is available here.

2. L.H. Ryder, Quantum Field Theory, 2nd eds., 1996; p. 412.

3. A.M. Polyakov, Gauge Fields and Strings, 1987; Section 4.3.

--

$^1$ Some authors (see e.g. Ref. 3 and this related Phys.SE post) use the terminology "compact $U(1)$ gauge theory" to stress that the gauge field takes values in a compact $U(1)$ Lie group rather than in a non-compact $u(1)$ Lie algebra. The latter is the standard QED formulation usually found in textbooks.