I'm working on the Eq.(7.57) in Peskin(page 236).
So I try to verify it with LSZ formula.
According to Eq (7.42)
So $\mathcal{M}(p \rightarrow p)=-Z M^{2}\left(p^{2}\right)$
In this I have two question：
① Consider S=1+iT, why did the "1" vanish?
② Is Eq.(2)->Eq.(3) correct?
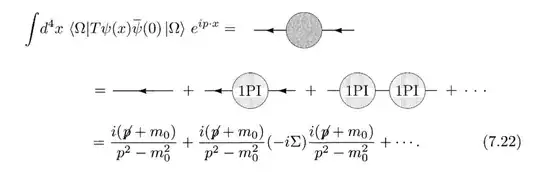
Consider Eq （7.22）in Peskin, it seems to lack a free propagator.
Eq.(2)= 1 + (1PI) + (1PI-1PI) + (1PI-1PI-1PI) + ...
Eq.(3)= (1PI) + (1PI-1PI) + (1PI-1PI-1PI) + ...
I think that your equality (2)=(3) is not correct. Moreover I am not sure what is the right interpretation of (3) in case of diagrams with exactly 2 exterior legs. Furthermore (4) seems to contradict the Kallen-Lehmann formula (see (7.9) in Peskin-Schroeder book). The latter implies that $$\int d^4x_1d^4x_2 e^{ip_1x_1}e^{-ip_2x_2}\langle\Omega|T\{\phi(x_1)\phi(x_2)\}|\Omega\rangle\approx (2\pi)^4\delta^{(4)}(p_1-p_2)\frac{iZ}{p_1^2-m^2+i\epsilon}.$$ Namely the exact propagator has a pole of first order as $p^2\to m^2$.
Another remark is that as far as I understand, in the Peskin-Schroeder book one particles states are assumed to be stable. That means in particular that $$\langle p_1|S|p_2\rangle=\delta^{(4)}(p_1-p_2).$$ That means that in the decomposition $S=1+iT$ the $1$ term is present, but the $iT$ term vanishes.
