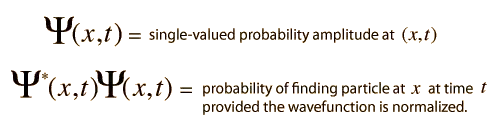The Born rule $$p=|\langle\psi|\phi\rangle|^2$$ defines the quantum probability and answers the question what is the probability that the measurement of $\psi$ will produce the outcome $\phi$? This is the standard interpretation of the formula but some authors, say, @Luboš Motl here and here apparently popularly claims just that “the word "interpretation" shoudn't be there at all”.
What is the generally accepted and experimentally supported reading of the formula? after all. What do experimentalists interpret in their labs? I've come across yet another derivation of the formula in the arXiv-preprint 1905.03332, but I'm sceptical about this because its author emphasizes at the end that even the probability is not needed here. There is only frequencies there. Is this yet another crazy?
It is common knowledge that the frequency interpretation of quantum probability is often criticized (Wallace, Zurek 2000's and others). On the other hand, additivity does really appear in many works on this topic. Even Gleason in the 1960s wrote on this, unless I'm mistaken. Could someone kindly (and precisely) comment on a relationship between the approaches? Probability vs frequencies, axiom vs derivation, and, preferably, the proposed `new derivation' of the rule through frequencies in the preprint above? (I'm not good in math).
PS. Does Zurek's derivation in the framework of decoherence solve the problem? My inclination is to believe that decoherence has already been confirmed in experiments many times and, perhaps, explains the transition under consideration because all the quantum systems are actually open at any one time.