Equivalent representations of path difference? (Laue equations and Bragg's law)

Question

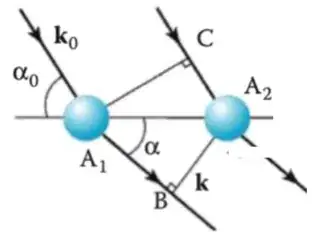
My textbook, Solid-State Physics, Fluidics, and Analytical Techniques in Micro- and Nanotechnology, by Madou, presents the following image and explanation in a section on x-ray diffraction and Laue equations:

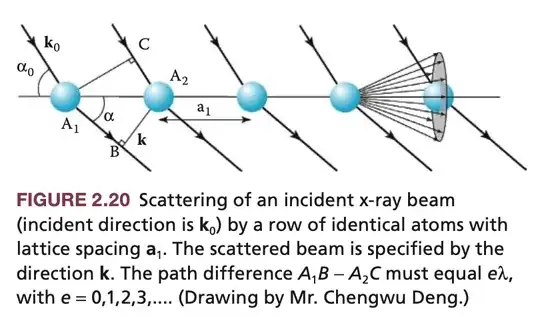
Constructive interference will occur in a direction such that contributions from each lattice point differ in phase by $2\pi$. This is illustrated for the scattering of an incident x-ray beam by a row of identical atoms with lattice spacing $\mathbf{a}_1$ in Figure 2.20. The direction of the incident beam is indicated by wave vector $\mathbf{k}_0$ or the angle $\alpha_0$, and the scattered beam is specified by the direction of $\mathbf{k}$ or the angle $\alpha$. Because we assume elastic scattering, the two wave vectors $\mathbf{k}_0$ and $\mathbf{k}$ have the same magnitude, i.e., $2\pi/\lambda$ but with differing direction. A plane wave $e^{i k \cdot r}$ is constant in a plane perpendicular to $\mathbf{k}$ and is periodic parallel to it, with a wavelength $\lambda = 2\pi/\mathbf{k}$ (see Appendix 2A). The path difference $A_1B − A_2C$ in Figure 2.20 must equal $e\lambda$ with $e = 0, 1, 2, 3, \dots$. For a fixed incident x-ray with wavelength $\lambda$ and direction $\mathbf{k}$, and an integer value of $e$, there is only one possible scattering angle $\alpha$ defining a cone of rays drawn about a line through the lattice points (see Figure 2.20).

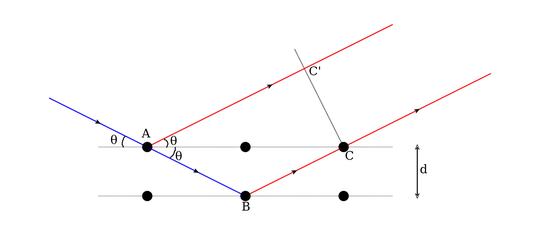
As you can see, it is said that the path difference is $A_1B - A_2C$. However, the Wikipedia article for Bragg's law seems to give a different definition for path difference:

(Author: M. Hadjiantonis)

There will be a path difference between the ray that gets reflected along AC' and the ray that gets transmitted along AB, then reflected along BC. This path difference is

$${\displaystyle (AB+BC)-\left(AC'\right)\,.}$$

If we think of these as vectors, so that $\vec{A_1B}$ is the vector from $A_1$ to $B$, and similarly for the others, then, visually, it seems to me that $\vec{A_1B} - \vec{A_2C}$ might be equal to $(\vec{AB} + \vec{BC}) - \left( \vec{AC'} \right)$, but I'm not totally sure.

Are these equivalent representations of path difference under Bragg's law, or are these actually different types of "path difference" for different concepts?

I would greatly appreciate clarification on this.

---

EDIT

I think I have found that the two definitions of path difference are proportional; that is, $A_1B − A_2C \propto {\displaystyle (AB+BC)-\left(AC'\right).}$

In the Wikipedia article for Bragg's law, it says the following:

The two separate waves will arrive at a point with the same phase, and hence undergo constructive interference, if and only if this path difference is equal to any integer value of the wavelength, i.e.

$${\displaystyle (AB+BC)-\left(AC'\right)=n\lambda \,,}$$

In addition to the textbook excerpt above, the authors go on to say the following:

Because crystals are periodic in three directions, the Laue equations in 3D are then:

$$\mathbf{a}_1 (\cos\alpha - \cos\alpha_0) = e \lambda$$ $$\mathbf{a}_2 (\cos\beta - \cos\beta_0) = f \lambda \tag{2.21}$$ $$\mathbf{a}_3 (\cos\gamma - \cos\gamma_0) = g \lambda$$

For constructive interference from a three-dimensional lattice to occur, the three equations above must all be satisfied simultaneously, i.e., six angles $\alpha$, $\beta$, $\gamma$, $\alpha_0$, $\beta_0$, and $\gamma_0$; three lattice lengths $\mathbf{a}_1$, $\mathbf{a}_2$, and $\mathbf{a}_3$; and three integers ($e$, $f$, and $g$) are fixed. Multiplying both sides of Equation 2.21 with $2\pi/\lambda$ and rewriting the expression in vector notation we obtain:

$$\mathbf{a}_1 \cdot (\mathbf{k} - \mathbf{k}_0) = 2 \pi e$$ $$\mathbf{a}_2 \cdot (\mathbf{k} - \mathbf{k}_0) = 2 \pi f \tag{2.22}$$ $$\mathbf{a}_3 \cdot (\mathbf{k} - \mathbf{k}_0) = 2 \pi g$$

with $\mathbf{a}_1$, $\mathbf{a}_2$, and $\mathbf{a}_3$ being the primitive vectors of the crystal lattice.

If we further define a vector $\Delta \mathbf{k} = \mathbf{k} − \mathbf{k}_0$, Equation 2.22 simplifies to

$$\mathbf{a}_1 \cdot \Delta \mathbf{k} = 2 \pi e$$ $$\mathbf{a}_2 \cdot \Delta \mathbf{k} = 2 \pi f \tag{2.23}$$ $$\mathbf{a}_3 \cdot \Delta \mathbf{k} = 2 \pi g$$

Dealing with 12 variables for each reflection simultaneously [six angles ($\alpha$, $\beta$, $\gamma$, $\alpha_0$, $\beta_0$, and $\gamma_0$), three lattice lengths ($\mathbf{a}_1$, $\mathbf{a}_2$ and $\mathbf{a}_3$), and three integers ($e$, $f$, and $g$)] is a handful; this is the main reason why the Laue equations are rarely referred to directly, and a simpler representation is used instead. The reflecting conditions can indeed be described more simply by the Bragg equation.

Further below we will learn that constructive interference of diffracted x-rays will occur provided that the change in wave vector, $\Delta \mathbf{k} = \mathbf{k} − \mathbf{k}_0$, is a vector of the reciprocal lattice.

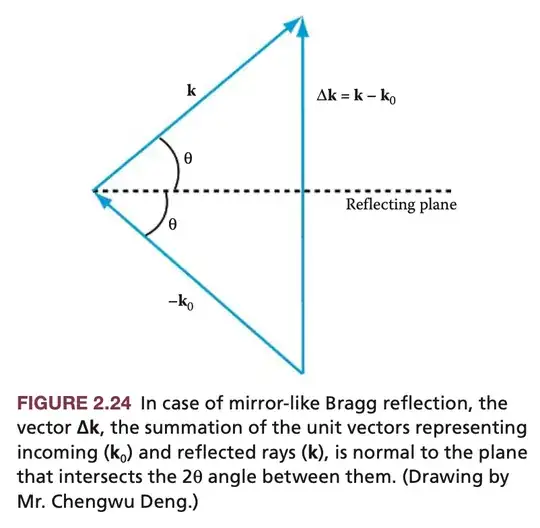
Bragg’s law is equivalent to the Laue equations in one dimension as can be appreciated from an inspection of Figures 2.24 and 2.25, where we use a two-dimensional crystal for simplicity. Suppose that vector $\Delta \mathbf{k}$ in Figure 2.24 satisfies the Laue condition; because incident and scattered waves have the same magnitude (elastic scattering), it follows that incoming ($\mathbf{k}_0$) and reflected rays ($\mathbf{k}$) make the same angle $\theta$ with the plane perpendicular to $\Delta \mathbf{k}$.

The magnitude of vector $\Delta \mathbf{k}$, from Figure 2.24, is then given as:

$|\Delta \mathbf{k}| = 2\mathbf{k}\sin(\theta)$

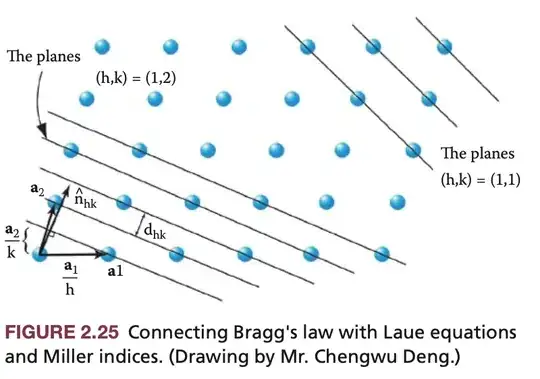
We now derive the relation between the reflecting planes to which $\Delta \mathbf{k}$ is normal and the lattice planes with a spacing $d_{hkl}$ (see Figure 2.25 and Bragg’s law in Equation 2.20). The normal unit vector $\hat{\mathbf{n}}_{hk}$ and the interplanar spacing $d_{hk}$ in Figure 2.25 characterize the crystal planes ($hk$). From Equation 2.23 we deduce that the direction cosines of $\Delta \mathbf{k}$, with respect to the crystallographic axes, are proportional to $e/a_1$, $f/a_2$, and $g/a_3$ or:

$$e/a_1:f/a_2:g/a_3 \tag{2.25}$$

From the definition of the Miller indices, an ($hkl$) plane intersects the crystallographic axes at the points $a_1/h$, $a_2/k$, and $a_3/l$, and the unit vector $\hat{\mathbf{n}}_{hkl}$, normal to the ($hkl$) plane, has direction cosines proportional to:

$$h/a_1, k/a_2, \text{and} \ l/a_3 \tag{2.26}$$

Comparing Equations 2.25 and 2.26 we see that $\Delta \mathbf{k}$ and the unit normal vector $\hat{\mathbf{n}}_{hkl}$ have the same directions; all that is required is that $e = nh$, $f = nk$, and $g = nl$, where $n$ is a constant. The factor $n$ is the smallest common factor of the integers $e$, $f$, and $g$ and is itself an integer. From the above, Laue’s equations can also be interpreted as reflection from the $h,k,l$ planes. From Figure 2.25 it can be seen that the spacing between the ($hk$) planes, and by extension between ($hkl$) planes, is given as:

$d_{hkl} = \dfrac{\hat{\mathbf{n}}_{hkl} \cdot \mathbf{a}_1}{h} = \dfrac{\hat{\mathbf{n}}_{hkl} \cdot \mathbf{a}_2}{k} = \dfrac{\hat{\mathbf{n}}_{hkl} \cdot \mathbf{a}_3}{l} \tag{2.27}$

Because $\Delta \mathbf{k}$ is in the direction of the normal $\hat{\mathbf{n}}$ and comes with a magnitude given by Equation 2.24, we obtain Bragg’s law from the Laue’s equations as:

$$\mathbf{a}_1 \cdot \Delta \mathbf{k} = \mathbf{a}_1 \cdot \hat{\mathbf{n}}_{hkl} 2k\sin(\theta) = 2 \pi e \tag{2.28}$$

or:

$$hd_{hkl} \dfrac{4 \pi}{\lambda} \sin(\theta) = 2 \pi e \tag{2.29}$$

and with $e = nh$:

$$2 d_{\text{hkl}} \sin(\theta) = n \lambda \tag{2.30}$$

In the Bragg equation we treat x-ray diffraction from a crystal as a reflection from reciprocal lattice planes rather than scattering from atoms. This construction has fewer variables than the Laue equations because reflections are wholly represented in two dimensions only.

So, if I am not mistaken, we have two different models that define the path difference in a crystal lattice equivalently up to a nonzero constant. Path difference in the Laue model is $A_1 B - A_2 C = e \lambda$, where, as was mentioned in the textbook, $e = nh$, where $n$ is the smallest common factor of the integers $e$, $f$, and $g$ and is itself an integer, and $h \not= 0$ is a miller index and therefore also an integer. Path difference in the Bragg model is ${\displaystyle (AB+BC)-\left(AC'\right)=n\lambda \,}$, where, based on page 50 of the textbook and what I have written regarding $n$ above (page 53), $n$ is defined identically as in the Laue model. Based on the physics of the situation, if I'm not mistaken, the wavelength $\lambda$ should be the same for both models. Therefore, we have that, for any crystal lattice:

$$A_1 B - A_2 C \propto (AB+BC)-\left(AC'\right),$$

since $n = \dfrac{e}{h}$.

Review and feedback is greatly appreciated.

Answer 1

The key idea to all these equations is the superposition of several $\cos$-terms. So let's quickly review this:

Suppose we have to waves $A_1 = \cos{(\alpha)}$ and $A_2 = \cos{(\beta)}$. If we add them together, we obtain $$ A_{tot}(t, x) = A_1(t, x) + A_2(t, x) = 2 \cos{(\frac{\alpha - \beta}{2})} \cos{(\frac{\alpha + \beta}{2})} % = \cos{(k x - \omega t)} % + \cos{(k x - \omega t + \varphi)} % = 2 \cos{(\varphi/2)} \cdot \cos{(\varphi/2)} $$ If we now set $\beta = \alpha + \varphi$, we obtain $A_{tot}= 2 \cos{(\frac{\varphi}{2})} \cos{(\alpha + \frac{\varphi}{2})}$. Note that for $\varphi=0, 2\pi, 4\pi, 6\pi, \ldots = n \cdot 2 \pi$, where $n$ is an integer, the first term becomes either one or minus one. Thus, the first term yields its max. or min value. In contrast, if $\varphi=\pi, 3\pi, 5\pi, 7\pi, \ldots = (2n+1)\pi$ the first term becomes zero. Thus, $A_{tot}$ becomes zero.

Now, all that we have to do it to translate this into a moving wave. The amplitude of this moving (plane) wave at the position $x$ at time $t$ is described by $A(x,t) = \cos{(k x - \omega t)}$, where for simplify I use the max. amplitude equal to one. If we add two such waves together, we obtain \begin{align} A_{tot}(t, x) &= A_1(t, x) + A_2(t, x) = \cos{(k x - \omega t)} + \cos{(k x - \omega t + \varphi)} \\ &= 2 \cos{(\varphi/2)} \cdot \cos{(k x - \omega t + \varphi/2)} \end{align} The important observation is that the first term is the same as above (it yields one if $\varphi$ is an even multiple of $\pi$ and zero if it is an odd multiple of $\pi$) and the second term oscillates -- in fact, the second term is just a plane wave. If you understand this, you understood the key idea of constructive and destructive interferences.

In order to relate this picture to your question, we have to ask ourself how the phase difference $\varphi$ is constructed. So let's take a look at your Figure 2.20

The incoming wave is a plane wave. Thus, if it reaches the point $A_1$ it is also at the point $C$. Thus, these two points always have a phase difference of zero, $\varphi_{A_1} - \varphi_C=0$. Since the outgoing wave is also a plane wave, the phase does not change beyond the line connecting the points $B$ and $A_2$. Hence, the phase difference is generated by the difference in length of the two path:

• The first path is from point $A_1$ to point $B$, and
• the second path is from point $C$ to point $A_2$

Thus, the path difference is $\overline{A_1B} - \overline{A_2C}$. Thus, the path difference is really just a length and not a vector In order to calculate $\varphi_{A_2} - \varphi_B$ we would use

• $\frac{C - A_2}{\lambda}= \frac{\varphi_{A_2}}{2\pi}$, and
• $\frac{A_1 - B}{\lambda} = \frac{\varphi_{B}}{2\pi}$

In order to understand these equations just think of the propagating wave: Every time the wave travelled the distance $\lambda$ the phase changed by $2\pi$.

The same logic applies to your second picture (Author: M. Hadjiantonis). However, here the first beam travels the distance from point $A$ to $C^\prime$, while the second beam travels from point $A$ first to $B$ and then to $C$. Again, the two outgoing waves are a plane waves. Thus, the their relative phase does not change after they pasted the point $C$ and $C^\prime$, respectively. Thus, their phase difference comes from the path difference, which is $\overline{ABC} - \overline{AC^\prime}$. I use $\overline{ABC}$, which is equal to $\overline{AB} + \overline{BC}$. Note, that these are not vector equations, but plain length.

The rest of your post is the same idea, but translated from two dimensions into three dimensions. You obtain all these complications, because we have to take all the different lattice planes into account, and we have to keep track of the three different lattice distances, i.e. $a_1$, $a_2$, and $a_3$. Simplifying matters I would say: A 3D crystal has a more complicated lattice structure compared to a 2D crystal, and each lattice plane reflect the incoming rays. Nevertheless, if we choose a single crystal plane, we still only calculate the path difference as above. If we don't choose a particular lattice plane

====

I had to check what common factor means, and I reckon I misunderstood it. However, since I saw that you are a mathematician, let me write it into physical terms and you translate it:

In order to obtain constructive interference from the $(hkl)$ lattice planes with lattice spacing $d_{hkl}$ the angle of reflection $\theta$ satisfies $$ n \lambda = 2 d_{hkl} \sin{(\theta)} $$ where $n$ is an integer. However, this is equivalent to $$ \lambda = 2 \frac{d_{hkl}}{n} \sin{(\theta)} = 2 d_{nh\, nk\, nl} \sin{(\theta)} $$ where $nh\, nk\, nl$ are the three Laue indices. E.g. let's consider $n=2$ and the $(1,1,1)$ lattice plane. The constructive interference can be either interpreted as

• the second order ($n=2$) reflection of the $(1,1,1)$ lattice plane with lattice spacing $d_{1,1,1}$, or
• as the first order ($n=1$) reflection of the $2,2,2$ lattice plane with lattice spacing $d_{1,1,1}/2$.

In this case $n$ is the largest common factor and I was wrong. Sorry!

Answer 2

Yes there is a direct correlation. Since this is a text book case, it is a simple case and you can actually solve it by using first year geometry. Not too tricky either.

I think you will find it to be a good exercise. Astronomy and optics rely heavily on geometry as a base and any opportunity to use it, keeps it sharp and ready. It's fundamental; both trig and algebra are based on it.

What I see are the triangles. We know a lot of things a triangles. In figure 2.20 we have two given angles and therefore the third angle.

A1B & BA2 (k) form a right angle which has it's own set of uses. A1B & A1A2 (a1) is the given angle (of refraction) A1C & A2C also form a right angle. and we are given A1B-A2C

Looking at your first Bragg's Law illustration we can see the differences of how the points are labeled and a new set of point designations should be used.

We see again a given angle of AB & AC and we can bisect AC from B at right angels.
There is a mirror quality with the deflection since the angels given above and below AC are the same.
So we can copy the bisection of AC finding a point B1 above AC so B1C are the same and so forth...

Just more fun stuff , I have found these sorts of exercises helpful in visualizing the information and visualizing is the foundation of what Einstein referred to as his "thought experiments".

Have fun.