Finding optimal angle for projectile, taking into account linear (Stokes) drag

Question

If you throw a projectile from the ground at a certain angle, it's not hard to see that, assuming we're in a vacuum, throwing it at 45º from the ground will always make it go farthest before it hits the ground again. I wanted to find out what's the optimal angle if we take into account air resistance.

Before I go on, let me say that there's really no point to this question. I'm not trying to solve a practical problem. I just thought it would be fun to try to solve the equations.

This is the model I'll use: We'll assume that air resistance is roughly proportional to velocity (aka. Stokes drag; this fails for high speeds/Reynolds numbers, so let's not go there); in symbols, $$\mathbf{F} = -k\mathbf{v}.$$ We'll throw the projectile with mass $m$ from $(0,0)$ with initial speed $v_0$, forming an angle $\alpha$ with the ground, and let's say $\gamma = k/m$ because it will turn up frequently.

The differential equations are:

$$\begin{align} \ddot{x} + \gamma \dot{x} &= 0 \\ \ddot{y} + \gamma \dot{y} &= -g \end{align}$$

with initial conditions $(x(0), y(0)) = (0,0)$ and $(\dot{x}(0), \dot{y}(0) )= v_0(\cos \alpha, \sin \alpha)$. Solving (assuming I haven't made any mistakes), we get:

$$ \begin{align} x &= \frac{v_0}{\gamma}\cos \alpha (1- e^{-\gamma t}) \\ y &= (\frac{v_0}{\gamma} \sin \alpha + \frac{g}{\gamma^2})(1-e^{-\gamma t}) - \frac{g}{\gamma}t. \end{align} $$

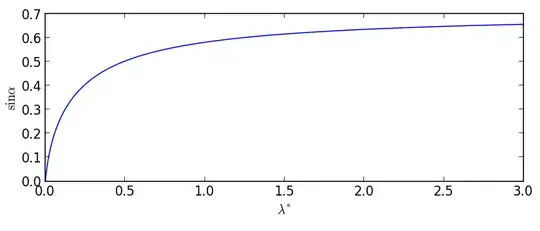
Now the thing to do would be to solve $y(t) = 0$, substitute that into $x$, differentiate with respect to $\alpha$ and set it equal to $0$. However, that gets messy quickly, because the solution involves the Lambert-W function and it's all a mess. I haven't even tried to substitute into $x(t)$.

So finally, my question is: is there a simpler or numerical way to solve this? Is there even a single angle which will always work, or does it depend on the conditions? Can we find that out without actually solving?

Answer 1

This is one of those problems that take on a much neater solution if you go dimensionless...

If you take a new time, $\tau$, horizontal coordinate, $\xi$, and vertical coordinate, $\eta$, such that

$$\tau = t \gamma,\ \xi = x \frac{\gamma}{v_0 \cos \alpha},\ \eta = y \frac{\gamma}{v_0 \sin \alpha}$$

you can rewrite your equations as

$$\ddot{\xi} + \dot{\xi} = 0$$ $$\ddot{\eta} + \dot{\eta} = -\frac{g}{\gamma v_0 \sin\alpha} = -\lambda$$

with initial conditions at $t=0$

$$\xi = \eta = 0,\ \dot{\xi} = \dot{\eta} = 1$$

This has solutions

$$\xi = 1 -e^{-\tau},\ \eta = (1+\lambda)(1 -e^{-\tau}) - \lambda \tau$$

and setting $\eta = 0$, we can get rid of $\tau$, and the range will be $\xi^*$ that fulfills

$$-\frac{1+\lambda}{\lambda}\xi^* = \log (1-\xi^*)$$

The maximum range will happen when $d\xi^*/d\alpha = 0$, so it is easy to show that at the maximum range:

$$\frac{d}{d\alpha}\frac{1}{\lambda} = \frac{1}{\lambda \tan \alpha}$$ $$\frac{d\xi^*}{d\alpha} = \xi^* \tan \alpha$$

Differentiating the equation for $\xi^*$ w.r.t. $\alpha$ using these two last formulas will, after a lot of cancelling and rearranging, take you to

$$\xi^* = \frac{1}{1+\lambda \sin^2 \alpha}$$

You can use this relation in the first expression we got for $\xi^*$ to get rid of $\xi^*$ and get a trascendental equation for $\alpha$ that looks something like:

$$\frac{\sin \alpha + \lambda^*}{\lambda^*}\frac{1/\lambda^*}{1/\lambda^* + \sin \alpha} = \log(1/\lambda^* +\sin\alpha) - \log(\sin \alpha)$$

where $\lambda^* = \lambda \sin \alpha$ and is independent of $\alpha$. This last equation you would want to solve numerically to get $\alpha^*$, the angle producing the maximum range.

While messy, the solution clearly depends on $\lambda^*$, so there will not be a single angle that always works.

EDIT Just run this last equation through a numerical simulation, and here's the optimal angle $\alpha^*$ (actually $\sin\alpha^*$) as a function of $\lambda^*$, showing how it grows ever closer to $\sqrt{2}/2$ for $\lambda^* \to \infty$.

Answer 2

I feel tempted to give a bit of a twist to this question. As John Rennie mentions in a comment above, unless you are talking about slowly moving microscopic projectiles, drag forces are best modeled as being proportional to the square of the velocity.

This brings me to a human-interest story relevant to the problem under discussion.

Last summer, it was reported that a 16 year old Indian schoolboy had solved a 350 year old problem that had stumped researchers since the time of Newton. All of this was highly over-hyped. The story, however, is relevant to the present discussion as one of the two problems solved by the boy is that of the movement of a particle under a uniform gravitational acceleration and a quadratic deceleration due to air resistance. You can find a Physics SE discussion here, and comments from professors at Dresden University (where the schoolboy did an internship) can be found here.

As OP is "seeking fun in solving equations", it might be worthwhile to check out some of the above links.

Answer 3

I built a high pressure (2000 PSI) pneumatic cannon that can shoot a 14 Oz finned aluminum projectile over 5 miles. After numerous tests the optimum angle proved to be 38 degrees. I roughly extrapolated a drag coefficient by comparing the measured distances with the so called ideal vacuum conditions, but it still does not explain the reason for the reduction from the ideal 45 degrees.