From a traveler's point of view, as he is accelerating with $1g$, in under one year he would reach the speed of light. Note that from his point of view, everything looks normal so he could keep accelerating, except of course other than all distances become zero and time looks frozen, and probably eventually points ahead of him would become his behind, and time started moving backward.
So, what prevents him from reaching speed faster than light?
This is the case of hyperbolic motion.
Let me shift the thought experiment to a related case.
In a linear accelerator a particle is accelerated by an electric field. You can accumulate kinetic energy as follows:
You create an electric potential that extends from the current position of the particle to some distance ahead of it. By the time the particle has traveled the extent of the potential you switch it off, and you set up a new potential, once again ahead of the traveling particle. You keep repeating that pattern.
Since this is a thought experiment there is no upper limit to the length of this linear accelerator.
So we have a particle traveling along the length of this linear accelerator, and with every stage of acceleration the particle accumulates more kinetic energy.
There is no upper limit to the amount of kinetic energy of the particle.
At each acceleration stage you can describe the physics in terms of some instantaneously co-moving frame, and at each acceleration stage the kinetic energy is increased.
Quantity of motion
The kinetic energy is a valid measure for what we can refer to as quantity of motion.
There is no upper limit to the quantity of motion, since there is no upper limit to the amount of kinetic energy that matter can accumulate.
I'm in favor of shifting to thinking of kinetic energy as the quantity of motion: no upper limit.
One more remark: kinetic energy isn't an intrinsic property. Kinetic energy is meaningful only in terms of relative motion. It's when an object impacts another object that kinetic energy comes in. The larger the relative velocity the larger the amount of kinetic energy that comes in.
Geometry of spacetime
According to Special Relativity the upper limit of velocity should not be seen as a property of matter, it should be seen as a geometric property of spacetime itself.
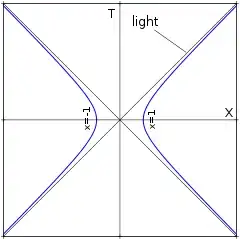
Image source: wikipedia hyperbolic motion image file
The image illustrates the geometric property.
The blue line represents the worldline of a point that is subject to uniform acceleration.
The vertical axis is labeled 'T' for time, the horizontal axis is labeled 'x' for position.
The blue line is the graph of the following expression:
$$ x^2 - T^2 = 1 $$
To ask: "In Minkowski spacetime, what prevents the particle from exceeding the speed of light?" is like asking: "Given the expression $ x^2 - T^2 = 1 $, what prevents the blue graph to cross over the black diagonal?
