In longitudional clock, for the return half tick why is the time in stationary frame less than the time in moving frame?

Question

I've just started special relativity and my textbook says $\Delta t_{stationary} \gt \Delta t_{moving}$. It proves this with mirrors placed perpendicular to the motion as shown:

In the above figure, two mirrors $A, B$ are inside a bus moving with velocity $v$ relative to the stationary frame.
In the moving frame(inside bus), $\Delta x = 2L$.
In the stationary frame, $\Delta x = 2D$.
Clearly the light travels more distance in the stationary frame and thus takes more time. Good so far.

Now, what happens if I put the mirror horizontally and shoot a light ray from the right side mirror as shown:

Clearly the light travels less distance in the stationary frame and thus takes less time. This means $\Delta t_{stationary} \lt \Delta t_{moving}$. Contradiction. What am I missing?

Answer 1

Your missing the second part of the the cycle.

Yes, the first half is shorter. But the light then bounces and returns back to the initial end, which by that time has moved further away. And since it’s had longer to move, the slow “tock” is a bigger effect than the short “tick” time: the net cycle time of the clock has lengthened and it runs slower.

So how can an observer moving with the clock see equal tick/tock periods? This gets to the difference in simultaneity between the two frames.

In the rest frame, you measure the time the light hits each end with two spatially separated clocks, then compare those to compute that the two directions take the same amount of time. The moving observer does the same thing and also sees equal times! How can that be? This happens because rest observer sees that the moving observers two separated clocks are not synchronized, with one reading ahead of the other.

Answer 2

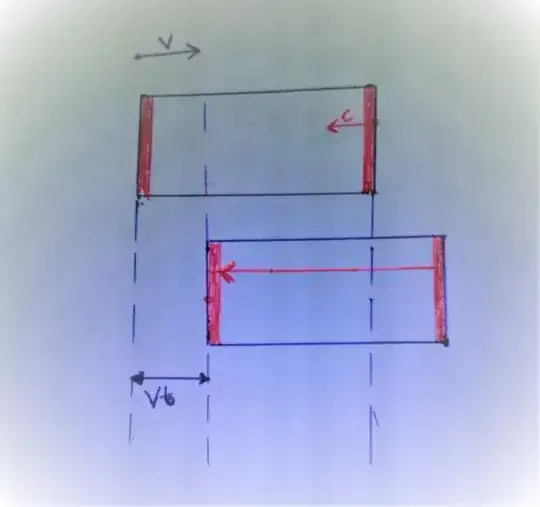
Your confusion comes from the fact that moving and stationary are relative terms. And that you are referring to distances inside the bus (moving as you say), as seen from inside the bus (from the rest frame of the bus).

Now let's say that the bus is the moving frame (relative to Earth ground) and there is a stationary frame (relative to Earth ground).

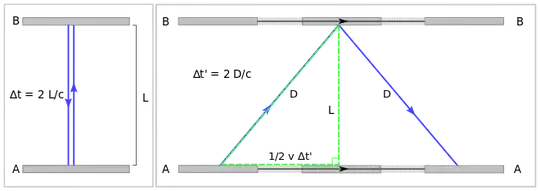
What you are trying here is a mirror clock. One tick is when a photon bounces between the two mirrors. Clearly, if the photon has to travel a longer distance between the mirrors, one tick will take more time. This means the clock ticks slower, time passes slower, but relative to what?

It is very important to understand that you can only talk about the relative passage of time, between two clocks. Let's say there is a photon clock on the moving bus (relative to Earth ground), and there is a stationary clock (relative to Earth ground).

In the moving bus, as seen from the stationary frame (this is what you confuse), a photon has to travel longer distance, 2D, thus a tick will take more time, thus time will pass slower in the moving bus as seen from the stationary frame. What we say is that in the bus, the photon clock ticks slower relative to the stationary clock.

But people (in the bus, comoving with the bus) looking at the clock in the bus, will see it tick normally.

It is only when they compare the clock to another clock (the stationary one) that they will see it tick differently. What will they see, which one ticks slower? People in the bus, comoving with the clock in the bus, will see the other clock (stationary clock) tick slower. Why?

Because speed is symmetrically relative. There is no universal reference frame. You can only talk about time dilation relative to another clock. This is SR.

Time dilation is a difference in the elapsed time measured by two clocks, either due to them having a velocity relative to each other, or by there being a gravitational potential difference between their locations. After compensating for varying signal delays due to the changing distance between an observer and a moving clock (i.e. Doppler effect), the observer will measure the moving clock as ticking slower than a clock that is at rest in the observer's own reference frame.

https://en.wikipedia.org/wiki/Time_dilation

Now you are asking about when the mirrors are moving parallel to the photon's direction of propagation and the answer is the same.

The right light clock ticks slower because half of the time, its right mirror is moving away from the photon, which takes longer to catch up with it.

What if a light clock travels perpendicular to mirrors that make up the clock?