This question does not have a close relationship to this or this Stack Exchange question. It's not about the Bohr atom model nor the Rutherford atom model, but is fairly closely related to this3 SE question.
Background to the question: The solutions to Maxwell's equations, with arbitrary time-independent sources $\rho (\vec x)$ and $\vec j (\vec x)$, are (from Jefimenko's equations, with a nod to @knzhou):
$$\vec E_{static} (\vec x) = \frac {1}{4 \pi} \int \frac {\rho(\vec x)} {|\vec x - \vec x'|^3} (\vec x - \vec x') d^3 x'$$
and
$$\vec B_{static} (\vec x) =\frac {1}{4\pi} \int \frac {\vec j (\vec x)} {|\vec x - \vec x'|^3} (\vec x - \vec x') d^3 x' ,$$
with arbitrary solutions $E_{rad} (\vec x, t)$ and $B_{rad} (\vec x,t)$ of the wave equation added:
$$ \vec E_{total} = \vec E_{rad} + \vec E_{static}.$$
$\vec E_{rad}$ and $\vec B_{rad}$ do not depend on $\rho (\vec x)$ or $\vec j (\vec x)$ at all, because $\rho (\vec x)$ and $\vec j (\vec x)$ are only position-dependent. In other words, $\vec E_{rad}$ and $\vec B_{rad}$ are merely “background radiation” allowed by Maxwell's equations but not resulting from the source terms $\rho (\vec x)$ and $\vec j (\vec x)$.
I will postulate source terms $\rho (\vec x)$ and $\vec j (\vec x)$, but represent $\vec j$ as follows:
$$ \vec j = \rho (\vec x) {\vec v}, $$ where $$\vec v = \vec v(\vec x). $$
In other words, the current is represented as if it were a fluid with density $\rho$ and position-dependent velocity. For charge conservation,
$$ \nabla (\rho \vec v) = 0.$$
The equations now describe the general static solution to Maxwell's equations, assuming that current is due to a charge density moving like a fluid.
Given the above assumptions, it is clear that $\vec v$ is a function of position, and I think it means that each element of $\rho$ is accelerated according to
$$\frac {d}{d t} \vec v = (\vec v \cdot \nabla) \vec v,$$ (corrected, thanks to @g.Smith) even though the charge and current densities per se are not time dependent. The flow of each charge density element taken in isolation would constitute a time-dependent current, but taken all together there would be no time dependence and therefore no radiation.
The question: I think the statements above are straightforward and correct. Now comes a bit of a leap:
If charge density $\rho$ has an associated mass density proportional to $\rho$, I believe a “fluid blob” of charge $\rho$ and current density $\rho \vec j$ could orbit a central, massive charge of opposite sign in such a way that the resulting charge and current density is time-independent and would not radiate. If it does not radiate, it is stable (I think).
This would seem to describe an almost-classical model of an atom, as long as total charge and angular momentum are quantized, and as long as no element of the charged fluid interacts with the rest of the charged fluid. (Classically this would be absurd, but we happily accept the quantum mechanical fact that the electron wave function does not interact with itself.) Surely this model has been explored and rejected for multiple good reasons, but I haven't been able to find any papers mentioning it.
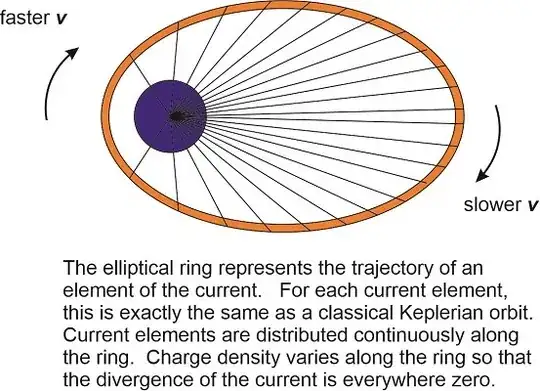
Here is a sketch of a simple case. The purple sphere in the center is the massive charge:
Based on references like Mfrisch, it seems that the system I've proposed has been considered and abandoned more because of its complexity than anything else. However, the problem is greatly simplified under the assumption that the charged fluid does not interact with itself. With a classical charged fluid that wouldn't make much sense; but since this is only a quasi-classical model it should be okay.
It may be possible to use a version of the Boltzmann equation to derive stationary charge/current distributions around a massive charged particle.