What happens in the double slit experiment if the detector is close to the slits?

Question

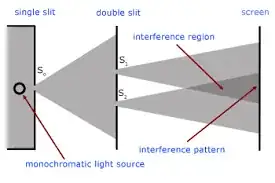
In the double slit experiment (with photons say) (see diagram below), what happens if the detector screen is moved close enough to the slits that the two light "cones" don't touch? Do the photons now cease to pass simultaneously through both slits?

Answer 1

No, they do not. Moreover, the interference is still there, but in a more complex form.

When the screen is close to $S_1$ and $S_2$ they are still a collection of point-like sources according to Huygens-Fresnel principle. You could integrate the contribution of each point within the slits and get the near-field interference. When you put the screen far away there is not much point in that integration, you could consider $S_1$ and $S_2$ just as two point sources.

Answer 2

That diagram is not correct.

There is no cone of light; light from each slit fills the entire space beyond the slits. That means that the "interference region" fills the entire space. There is no special region where there is interference, outside of which there is not.

Close to the screen the intensity of the light might be weak, and interference will have a more complex pattern than in the far field, but it's there nonetheless.

Answer 3

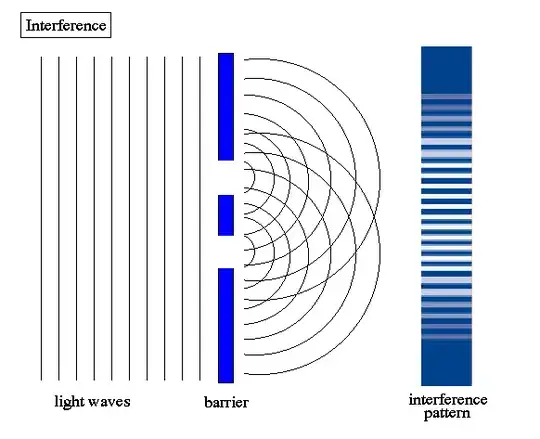
As noted in the other answers, the diagram is somewhat misleading. A more accurate picture is shown here:

The waves through the slits spread out in all directions. (As pointed out in the comments, the amplitude is much larger in the "forward" directions when the width of the slit is much larger than the wavelength of the light, which is perhaps what your original diagram was trying to convey. Even so, there is still some small wave amplitude in most directions from the slit.)

The reason we usually don't care about the waves spreading out at large angles (beyond their smaller amplitude, as noted above) is that it allows us to use the Fraunhofer approximation, which assumes that we are at a large distance from the screen (compared to the size of the pattern in the screen.) In the region you indicate, we are not necessarily at a "large" distance from the screen, and so we would need to use the Fresnel approximation instead. The mathematics required to analyse this case are rather more complicated, and so it's usually skipped in an introductory physics course.

Finally, nothing that I've said here requires the light to behave quantum-mechanically or classically. The only difference is that if we think of the light as being composed of photons, the intensity pattern should be treated as a probability distribution.

Answer 4

Bricmont (Quantum Sense and Nonsense, 2017, pp.22-23) explicitly says that the interference disappears if the slits and detector are too close, but the consensus appears to be the converse. I only add this for the record.

Answer 5

If the screen is so close to the slits that the two "cones" don't overlap and land on separate areas of the screen, it is obviously easy to know which slit each photon goes through. No interference fringes will appear.

However there is still temporal interference, because there is an "anticorrelation" between photon counts in the areas where photos hit the screen. That is, if the beam illuminating the slits is so dim that it can be considered to be a stream of single photons, and if the detectors are sensitive enough and fast enough to distinguish single photon arrivals, detectors in those two areas will never detect a photon at the same time. A plot of photon counts over time for each detector will look (and be) random, but plots of the two sets of counts will be "opposite".