What will happen to a ball kept on a frictionless inclined plane?

Question

I was wondering about this question since I learned about rolling motion in the chapter on rotational mechanics. I was unable to come to a solid conclusion due to the reasons mentioned below.

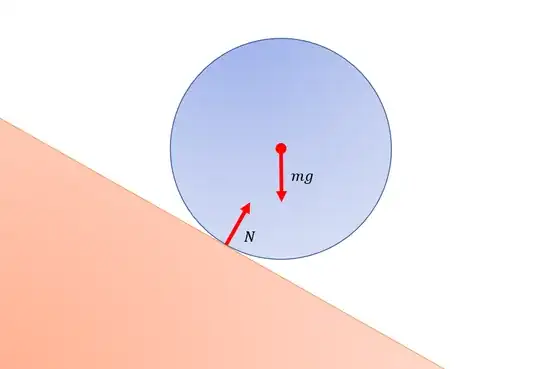
The following diagram shows a ball on a frictionless inclined plane and the forces acting on it:

The forces acting on the ball are shown in red and are the normal contact force $N$ and the gravitational force of attraction $mg$. I qualitatively determined the torque of these forces about two axes - one passing through the centre of mass of the ball of uniform density, and the other passing through the point of contact of the ball and the inclined plane. Both of these axes are perpendicular to the screen.

When the axis passes through the centre of the ball, the torque exerted by $mg$ is zero as its line of action meets the axis. Further, the torque exerted by $N$ is also zero due to the same reason. There are no other forces. So, net torque about this axis is zero, and this tempts us to conclude the ball slides down the inclined plane.

When the axis passes through the point of contact, the torque exerted by $N$ is zero but the torque exerted by $mg$ is non-zero. This means the ball must roll i.e., it rotates while moving down the inclined plane. This conclusion is contradictory to the former case.

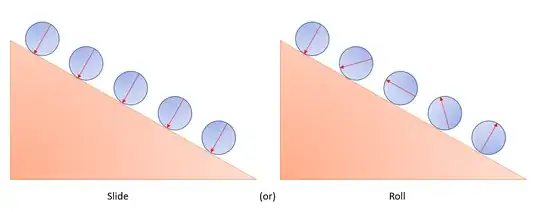
So, what exactly will happen to a ball kept on a frictionless inclined plane - will it slide or roll?

The following diagram is a visual interpretation of my question (if the terms slide and roll confuses the reader) where the red arrow denotes the orientation of the ball:

^{Image Courtesy: My own work :)}

---

^{Please Note: The question - Ball Rolling Down An Inclined Plane - Where does the torque come from? discusses the case of ball rolling on an inclined plane where friction is present. Since the question - Rolling in smooth inclined plane is marked as duplicate of the former, and has no sufficient details, I planned to ask a new question with additional information.}

Answer 1

...the torque exerted by $N$ is zero but the torque exerted by $mg$ is non-zero. This means the ball must roll...

Actually, it means that the angular momentum about that axis must increase. That is not the same as rolling. If the axis is through the center of mass of the object then the only way for the angular momentum to increase is through rolling. However, if the axis does not pass through the center of mass then there is also angular momentum due to the linear motion. In other situations this is the difference between orbital angular momentum and spin angular momentum. So let's calculate the "orbital" angular momentum in this problem.

The torque is $m g R \sin(\theta)$ where $R$ is the radius of the ball and $\theta$ is the angle of the incline.

The magnitude of the "orbital" angular momentum is given by $R m v$ where $v$ is the linear velocity of the center of mass, so its time derivative is $R m a$ where $a$ is the linear acceleration of the center of mass.

From Newton's laws the linear acceleration is the component of gravity which is down the slope. This is $ma=mg \sin(\theta)$ so $a=g \sin(\theta)$.

Substituting the linear acceleration into the time derivative of the orbital angular momentum gives $R m g \sin(\theta)$ which is equal to the torque. This means that the increase in angular momentum due to the torque is fully accounted for by the increase in the "orbital" angular momentum and there is no left over torque for increasing the "spin" angular momentum. Therefore, the ball does not spin/roll regardless of which axis you examine.

Answer 2

So, what exactly will happen to a ball kept on a frictionless inclined plane - will it slide or roll?

Frictionless means the surface of the incline cannot exert any torque on the ball. By Newton's second law, that means the state of rotation of the ball remains unaltered, specifically:

• if the ball was spinning at angular velocity $\omega$ then it will simply continue to do so: $\frac{\text{d}\omega}{\text{d}t}=0$.
• if the ball wasn't spinning at all ($\omega=0$) then sliding down the frictionless incline will not alter $\omega$ . Again $\frac{\text{d}\omega}{\text{d}t}=0$.

For any change in rotational status to occur, a torque $\tau$ needs to act on the ball, so that:

$$\tau=N\mu$$

but with $\mu=0$, $\tau$ is always $0$.

Answer 3

to see what happened, let's look at the equations of motion:

$$m\,\ddot{s}+F_c-m\,g\sin(\alpha)=0\tag 1$$ $$I_b\,\ddot{\varphi}-F_c\,R=0\tag 2$$

case I: Ball is rolling without slipping:

$$\ddot{s}=R\ddot{\varphi}\tag 3$$

You have three equations for three unknowns $\ddot{s}\,,\ddot{\varphi}\,,F_c$

you obtain:

$$\ddot{\varphi}=\frac{m\,g\,\sin(\alpha)\,R}{m\,R^2+I_b}$$ $$\ddot{s}=R\ddot{\varphi}$$ $$F_c=\frac{I_b\,m\,g\,\sin(\alpha)}{m\,R^2+I_b}$$

case II: Ball is sliding :

This is your case, because you don't have the contact force $F_c$.

In this case the contact force $F_c$ is equal zero.

$$m\,\ddot{s}=m\,g\sin(\alpha)$$ $$I_b\,\ddot{\varphi}=0\quad \Rightarrow \varphi=0$$

case III: Ball is rolling :

Instead of equation (3) you have now the equation for a friction force

$$F_c=\mu\,N=\mu\,m\,g\,\cos(\alpha)$$

you obtain:

$$\ddot{s}=g(\sin(\alpha)-\mu\,\cos(\alpha))$$

$$\ddot{\varphi}=\frac{\mu\,m\,g\,\cos(\alpha)\,R}{I_b}$$

so if $\mu=0$ the ball is sliding which is case II.

Answer 4

The ball will slide. You mistake was to choose an 'accelerating axis' (The point of contact through which the axis passes is accelerating). Note that the you can only form torque equation about the axis which are stationary or translating with constant velocity.

The beauty of centre of mass is that torque equation can be applied to an axis passing through C.O.M irrespective of whether that axis is accelerating or not. (That's why C.O.M is the most popular choice for applying torque equation). This property is only true for centre of mass only. (You should try to prove it)

In order to get correct equations you must apply pseudo forces on all the particles on the rigid body (try it!). Then you must find the torque due to the applied pseudo force (I call it 'pseudo-torque').

It is very easy to show (I will leave this an an exercise to you) that the torque due to all the pseudo forces can be obtained by considering the pseudo force acting alone at the Centre of Mass of rigid body.

EDIT: Meaning of accelerating axis: Imagine particles on the rigid body through which the axis of rotation pierces. Then the particles of the rigid body through which is axis pass may accelerate taking the axis along with them.

The acceleration of the axis is same as that of the particles through which the axis pierce.

Imagine yourself sitting on the moving axis (more precisely,attach a translating frame to the moving axis), an amazing property of the rigid body is that you will observe the entire body rotating about that axis and the angular velocity of rotation will be same for all set of of points through which you chose to pierce your axis of rotation.

Answer 5

I think much of the confusion comes from the false notion that a moment [or torque, I use these words synonymously, compare Moment (Physics)] might have an axis or a place. In classical mechanics, such a torque is associated with any rigid body, rather than with a specific place on that body.

Strict method

Usually, you would cut the rigid body free from its surroundings, thus introducing border forces that act upon it, in addition to any volume forces that result from a force field like gravity, and possible torques that are applied externally.

Then, to determine the body's change of motion, you would separate forces from torques by displacing forces perpendicular to their line of effect, so that all of them finally affect the body's center of mass (CoM). For each displaced force, you will have to introduce a compensating displacement torque: while moving a force along its line of effect has no physical implications, moving it any other way does.

Once you have finished displacing all forces the the body's CoM, you will sum up all forces to get the total force acting upon the body's CoM. Much in the same way, you will sum up all the displacement torques and any torques that apply externally, and the result will be the total torque that affects the body. You can denote your torque with a circular arrow anywhere in your diagram, it makes no difference where you put it.

Applying this to your example, you are already done with the first diagram: All forces' lines of effect intersect in the ball's center. There is nothing to do, and the torque is zero. The ball will slide.

Intuition

It is counter-intuitive to accept that an amount of torque applied in one place should have the same effect on a rigid body as the same amount of torque applied in another place of the same body: Intuition dictates that the body should start rotating around the axis where the torque is applied.

However, this is only true if said axis is in the body's CoM. A body will always and only rotate about its CoM if no other force is applied.

Think of a wheel with an axle that is not in the middle, but, say, slightly off. If you suspend this axle in a fixed and rigid frame and then apply a torque, the wheel will most definitely start spinning around the axle, and the wheel's CoM will rotate around the axle, too. However, your suspension will consequently experience and exert a force to the axle, rotating at the same speed as the wheel. This is called excentricity. Now imagine to suddenly let the wheel loose. It will continue to move with its CoM's momentary velocity and continue spinning around its CoM, which is not on the axle. Hence, you will have a flying wheel, generally on a parabolic curve and its axle will rotate around its CoM. Note that the wheel will then not spin around said axle any longer, because with the suspension gone, there is nothing left to apply any force to it.

Answer 6

Several people have suggested that the contact point will act as an axis. I don't see how this is the case, since it's in no way constrained. For example, the axle of wheel is constrained by being attached to a car or bike, thus if you push on the rim that force gets turned round the axle. If I push a person (standing on normal ground) near his CoG, that person's feet are constrained by friction and he'll rotate about them - he'll tip or even fall over.

The contact point between the ball and the surface isn't constrained either by a rod through it or by friction, so it's no more likely to act as an axis than any other point. To go back to my pushing a person analogy, it's like he's wearing ice skates and I push him in the direction they're pointing - he won't topple, he'll slide.

I can't post comments, so I'm putting it here.

Answer 7

Roll a toy car along a surface, at any angle, and the wheels rotate. That's because friction is applying a force at the contact point between the wheels and the surface.

Now move it parallel to the surface, a few cm away. The wheels do not rotate because there is no force at the contact point. The reason there's no force is because there's no friction (in this case because it's not touching), on a frictionless surface there'd be no friction even if you were touching it because, well, it's frictionless.

Answer 8

Torques and system's angular momentum must be measured relative to some origin.If the center of mass of the system is not accelerating relative to an inertial frame,that origin can be any point.However,if it is accelerating then it must be the COM.So assuming an axis at the point of contact is not right.

And the ball will definitely slide..

Answer 9

The ball will roll. The centre of mass of the ball is not vertically above the point of contact, so there is nothing to prevent it from falling vertically.

The two conclusions you mention are not contradictory- you have simply misunderstood their implications.

There is no turning moment about the centre of the ball.

There is a turning moment about the point of contact. That will cause the ball to rotate about the point of contact, the effect of which is to cause the ball to rotate also about its centre of mass.

It is nonsense to say that friction is required for a turning moment to occur. Suppose you replace the ball with a pencil leaning normally to the slope. The pencil will not slide down the ramp, leaning all the while, it will topple and then slide. The toppling happens as a consequence of the turning moment around the point of contact.

To press the point, consider a leaning pencil on a flat frictionless surface. The pencil will of course rotate and topple. The absence of friction facilitates rather than hinders the rotation.

The reason why falls on ice are common is precisely that the absence of friction makes it impossible to counter the turning moment around ones point of contact with the ground if one does not remain sufficiently upright. The effect is worse on a sloping icy surface than on a flat one.