Work Done by a Car Pulling a Sled

Question

Is work still equal to force times distance if there is no acceleration?

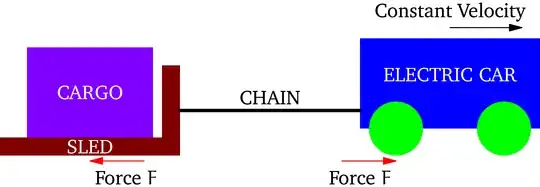
Consider an electric car pulling a sled at a constant velocity as shown. The static friction force $F$ at the wheels is equal to the sliding friction force on the sled. Since the forces are balanced, there is no acceleration.

Assume a distance $D$ is traveled at this constant velocity. The work done by the car is force times distance, or $W=FD$.

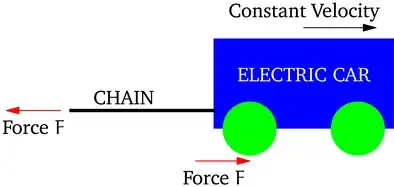
In this scenario, the tension in the chain will also be equal to the force $F$ as shown below.

I believe the diagram below is enough to determine the work done by the car. The details of the sled are not important. The work done by the car is $W=FD$ regardless if there is a sled at the end of the chain, a trailer with its brakes applied, or a person pulling on the chain. The force in the chain is sufficient to calculate the work done by the car.

Now suppose that the force in the chain increases to $2F$ while the car increases its power output to maintain the constant velocity. I contend that the work done by the car doubles for the same distance traveled, $W=2FD$.

Am I correct so far?

Compare this scenario of a car with a similar question regarding work done by a dog on a leash. Is it more work to put more (apparent) effort to get the same outcome? In this question, the car is replaced by a dog and the sled is replaced by a walking person.

I contend that, for a given walking distance, the dog will do more physics work when the leash force is greater. I understand that the dog will also do extra work because - unlike the car - it is not 100% efficient. For example, the dog will be jumping around and wasting some energy.

There are many reasons people in the other question give for why the dog's physics work is NOT increased when the leash force is higher, including...

1. The person is not moving faster when the dog pulls harder.
2. The person is walking. If the person was sliding then the work would be higher.
3. "Force is mass times acceleration. If you are pulling harder but not actually speeding up, then it isn't force."

None of these reasons seem correct to me, but they seem to be the majority opinions in the question about dogs. Can someone clear up my (or their) misunderstanding?

Answer 1

You are 100%, unequivocally and unambiguously correct. For a constant force in the same direction as a displacement $D$, $$W=FD.$$ Period.

The idea that where the energy goes--into heat, kinetic energy, potential energy, etc.--is relevant to the calculation of work is flat wrong.

The idea that the "motion of the center of mass" is relevant to the calculation of work in any other way than insofar as it has an effect on $D$ is also flat wrong.

Answer 2

I believe the diagram below is enough to determine the work done by the car. The details of the sled are not important.

One issue I have with your analysis is that it neglects what was needed in order to have the car pulling the sled at constant velocity. Initially, the car had to exert a net force to the right in order to accelerate the sled and achieve the stated velocity. Once that velocity is reached, the car can reduce its pulling force to match the opposing force exerted by the shed, for a net force of zero, so that now the car and sled are moving and constant velocity and the net work done being done on the sled from that point on is zero. In short, net work had to be performed on the sled by the car to attain the constant velocity (kinetic energy) of the sled, per the work energy principle.

Now let's look at the person walking the dog. Let us say the dog is not exerting any force on the person while the person is walking. In effect, the leash is slack. The person is walking at a constant velocity of 1 m/s with no tension on the leash. The dog sees a cat and lunges forward in an attempt to chase the cat putting tension on the leash. But the person exerts an equal but opposite force on the leash to restrain the dog, and in so doing the persons velocity does not change. In contrast to the car-sled scenario, in this scenario at no time did the dog perform net work on the person.

In the car-sled scenario, the total work done by the car includes that which accelerated the sled from zero velocity to some final velocity. In the dog-person scenario the total work done by the dog does not include any work to accelerate the person to the final velocity. The analogy for the car-sled is the driver of the car steps on the gas pedal attempting to accelerate the car, but for some reason the sled keeps it from accelerating. Gas is wasted. When the dog attempts to accelerate the person and it doesn't happen, the additional energy it expends is wasted.

I would like to say, in connection with the previous post that motivated this post, I don't believe there is a completely right or wrong answer. It was never my intention to say the dog is not doing any work in pulling on the person who is walking at constant velocity. My point was that if the dog expends additional energy attempting unsuccessfully to accelerate the walker (and catch the cat), it is to no avail and the additional effort is wasted. That was my only point.

Hope this helps.