Why is the spin-orbit interaction for a nucleus so much more important than the spin-orbit interaction in atomic physics?

Question

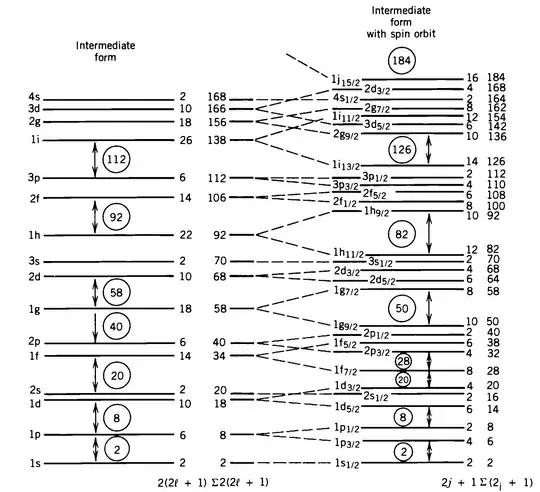
In atomic physics, the spin-orbit is a small correction between 1/1000 and 10ppm, so fairly small. In contrast, in nuclear physics the inclusion of the spin-orbit interaction is necessary to reproduce the basic level scheme, see picture below (from Kenneth Krane, Introductory Nuclear physics). Why is that?

I imagine it has to do with the $r$-dependence: In a semi-classical calculation, the energy correction due to the spin-orbit interaction has a $1/r^3$ dependency. However, I have only seen this calculation for the atomic case and not for the nuclear one.

Answer 1

The nuclear force is inherently spin-dependent, which is why the interaction between nucleons is different, depending on whether spins are parallel or not:

The nuclear force is not simple, though, as it depends on the nucleon spins, has a tensor component, and may depend on the relative momentum of the nucleons.

(quoted from Wikipedia, which cites here the book by Krane, mentioned in the OP.)

Related: Why nuclear force is spin dependent?

Answer 2

To self-answer my question:

Yes, it is indeed because of the $1/r^3$ dependency of the spin-orbit interaction. Intuitively speaking, in the atomic case the electron orbits the nucleus on the order of $10^{-10}$m. In the nuclear case, one nucleon orbits another one with a distance on the order of $10^{-15}$m.

Another more mathematical point of view is that considering a series expansion of all the forces involved, the spin-orbit-interaction is a higher order term and thus scales with $\nabla^n F$. Since $F$ is much more close-ranged for the nucleus, $\nabla^n F$ is much higher and contributes more strongly.