Pair production - mathematically?

Question

Allover the web i am only seeing a statement similar to this:

Pair production is not possible in vaccum, 3rd particle is needed so that conservation of momentum holds.

Well noone out of many writers shows, how to prove this matematically. So this is what interests me here.

---

First i wanted to know if pair production really cannot happen in vacuum, so i drew a picture and used equations for conservation of energy and conservation of momentum to calculate energy of a photon $(h \nu)$ needed for pair production.

It turns out $h\nu$ is different if i calculate it out of conservation of energy or conservation of momentum. And even more! It can never be the same because equallity would mean parts $v_1 \cos \alpha$ and $v_2 \cos \beta$ should equall speed of light $c$. Well that cannot happen.

Below is my derivation.

---

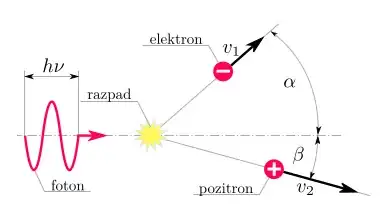
CONSERVATION OF ENERGY: $$ \scriptsize \begin{split} W_{1} &= W_{2}\\ W_f &= W_{e^-} + W_{e^+}\\ h\nu &= W_{ke^-} + W_{0e^-} + W_{ke^+} + W_{0e^+}\\ h\nu &=\left[m_ec^2 \gamma(v_1) - m_ec^2\right] + m_ec^2 + \left[m_ec^2 \gamma(v_2) - m_ec^2\right] + m_ec^2\\ h\nu &=m_ec^2 \gamma(v_1) + m_ec^2 \gamma(v_2)\\ h\nu &=m_ec^2 \left[\gamma(v_1) + \gamma(v_2) \right]\\ \end{split} $$

---

CONSERVATION OF MOMENTUM:

$y$ direction: $$ \scriptsize \begin{split} p_{1} &= p_{2}\\ 0 &= p_{e^-} \sin \alpha - p_{e^+} \sin \beta \\ 0 &= m_e v_{1} \gamma(v_{1}) \sin \alpha - m_e v_{2} \gamma(v_{2}) \sin \beta\\ &\text{If $\boxed{\alpha = \beta} \Longrightarrow \boxed{v_1 = v_2}$ and:} \end{split} $$

$$ \begin{split} \scriptsize 0 = 0 \end{split} $$

$x$ direction:

$$ \scriptsize \begin{split} p_{1} &= p_{2}\\ \frac{h}{\lambda} &= p_{e^-} \cos \alpha + p_{e^+} \cos \beta \\ \frac{h \nu}{c} &= m_e v_{1} \gamma(v_{1}) \cos \alpha + m_e v_{2} \gamma(v_{2}) \cos \beta\\ h \nu &= m_e c \Big[ \gamma(v_1) \underbrace{v_{1} \cos \alpha}_{\neq c} + \gamma(v_{2}) \underbrace{v_{2} \cos \beta}_{\neq c} \Big] \end{split} $$

Alltogether:

Because momentum in $y$ direction equals 0 (holds for some combinations of $\alpha, \beta, v_1, v_2$) whole momentum equals just the momentum in $x$ direction. So if i add them i get:

$$ \scriptsize h \nu = m_e c \Big[ \gamma(v_1) \underbrace{v_{1} \cos \alpha}_{\neq c} + \gamma(v_{2}) \underbrace{v_{2} \cos \beta}_{\neq c} \Big] $$

---

From this i can conclude only that i cannot sucessfully apply conservation of energy and conservation of momentum at the same time and therefore pair production in vacuum cannot happen.

QUESTION1: Why do writers state that 3rd particle is needed so that conservation of momentum holds? What if conservation of momentum holds and conservation of energy doesn't? How can we say which one holds and which one doesnt?

QUESTION2: Do writters actually mean that if a 3rd particle is included we can achieve $h \nu$ to match in both cases?

QUESTION3: Can someone show me mathematically how this is done? I mean it should right?

Answer 1

Conservation of energy and conservation of momentum cannot really be separated, since energy and momentum are just different components of a relativistic 4-vector; different inertial observers will "split" this 4-momentum into energy and momentum in different ways, much like they will "split" spacetime into space and time in different ways.

The real reason spontaneous pair production cannot happen is that in Minkowski spacetime two future-directed timelike vectors (like the 4-momenta of the produced pair) must always add to a future-directed timelike vector. You can convince yourself of this by graphically considering the vectors, which lie in the interior of the future-directed timelike cone, and of course it can also be shown analytically. (If I recall correctly The geometry of Minkowski spacetime by Gregory Naber has a nice proof of this.)

This total 4-momentum must be equal to the initial 4-momentum of the photon by the (inseparable) conservations of momentum and energy. The 4-momentum of the photon, however, is a lightlike (null) vector, which rules out the spontaneous pair creation.

So why is "assisted" pair creation possible? If you have a third particle then the final situation has three timelike, future-directed timelike 4-momenta to consider, so the total 4-momentum is timelike and future-directed as before. The initial 4-momentum, on the other side, is now the sum of a lightlike, future-directed one (the photon's) and a timelike, future-directed one (the third particle's), and this results in a timelike vector. Thus assisted pair production can happen.

Answer 2

Question 3:

One time and two space dimensions for simplicity (t, x, y). Photon travelling in +x direction. Photon four momentum is $(\frac{E}{c}, p_x, 0)$. It's null so $$ \frac{E^2}{c^2}-p_x^2=0$$ So $$p_x = \frac{E}{c} $$ $E=h\nu$, so photon four momentum is $(\frac{h\nu}{c}, \frac{h\nu}{c}, 0) $

To keep it simple, assume the electron/positron are emitted at equal angles to the x axis. One of them (the electron say) has four momentum $$(\frac{E_e}{c}, p_ecos\phi, p_esin\phi) $$ which, being timelike, satisfies $$\frac{E_e^2}{c^2}-p_e^2 = m_e^2c^2 $$ Conservation of momentum in the x direction: $$ \frac{h\nu}{c} = 2p_ecos\phi = 2\gamma_vm_evcos\phi \ \ (0)$$ where $v$ is the electron/positron velocity magnitude. So $$ h\nu = 2\gamma_vm_ev \ c \ cos\phi \ \ (1)$$ So clearly $$ h\nu < 2 m_e c^2$$ However, the photon must supply at least the electron and positron rest masses, so $$h\nu > 2m_e c^2 \ \ (2) $$ Therefore for (1) to be satisfied, the x momentum must have gone somewhere else. The nuclear recoil accounts for this.

Answer 3

For simplicity, take a particle with mass 2 units and speed v1=[v1x,v1y(=0)] splitting symmetrically into two equal masses of 1 unit each and speed v2=[v2x,+/- v2y]. Next apply momentum and energy conservation to the start and finish states. Momentum:
p1x=2v1x; p2x=v2x +v2x =2v2x; for these to be equal; v1x=v2x. p1y=0 (given); p2y=v2y – v2y=0 (symmetry), the two momenta are equal. Energy: e1x=2 v1x ^2 ; e1y=0 (given); Total e1t=2v1x ^2.
e2x=2v2x ^2; e2y=v2y ^2+(-v2y)^2=2v2y^2; Total e2t=2v2x ^2+2v2y^2.
As v1x=v2x from above, we have e2t=2v1x ^2+v2y ^2= e1t+2v2y ^2. Since the last term is positive, to make e1=e2 , we must have v2y=0. That means it is not possible to split particles with mass and energy to go away from each other if their momentum and energy are conserved. Thus there must be a third particle involved. Since energy is always positive, the only possibility is to add +/- p to the system to balance both energy and momentum. There is no net momentum change after splitting as the momentum total is zero due to the sign change. That says to split a stream of particles we need a catalyst that doesn’t contribute to the overall balance and helps in the splitting. This can be seen in many areas of physics like the splitting of a fluid jet and the formation of vortices. In particle physics the electron and the positron can be looked at in a similar manner. The e-p pair will revert into radiation again if they don’t go away from each other.