I'm studying deep inelastic scattering, and currently at the part where they say the Callan-Gross relation:
$$F_1 (x) = \frac{1}{2x} F_x (x)$$
where $F_1$ and $F_2$ are the dimensionless structure functions, tests that quarks have spin $\frac{1}{2}$. Why is this the case? I do not understand it. If it is too long to explain, is there a complete derivation for other spin cases, so that I can read it myself?
Thank you!
For inelastic scattering, the cross section can be modeled like this:
$$ \left( \frac{\text{d}^2\sigma}{\text{d}\Omega\text{d}E} \right) = \left( \frac{\text{d}\sigma}{\text{d}\Omega} \right)_\text{Mott}\, \left[ W_2(Q^2,\nu) + 2W_1(Q^2,\nu) \tan^2 \frac{\theta}{2} \right] $$
where the first term corresponds to the electric part and the second one (angle dependent!) corresponds to the magnetic one. For spin-$0$ particles, we only have the first term (This will be important later). We can rewrite this in terms of dimensionless structure functions, $F_{1,2}$,
$$ \left( \frac{\text{d}^2\sigma}{\text{d}\Omega\text{d}E} \right) = \left( \frac{\text{d}\sigma}{\text{d}\Omega} \right)_\text{Mott}\, \left[ \frac{1}{\nu}F_2(x,Q^2) + \frac{2}{M}F_1(x,Q^2) \tan^2 \frac{\theta}{2} \right] \tag{1} $$
where
$$ F_1(x,Q^2) = M\, W_1(Q^2,\nu)\quad\text{and}\quad F_2(x,Q^2) = \nu\, W_2(Q^2,\nu) $$
and $x=\frac{Q^2}{2M\nu}$ is the Bjorken scaling. These dimensionless structure functions do not depend strongly on the momentum transfer $Q^2$, hence one can deduce that the particles in question (i.e. the quarks) are pointlike$^1$. So let's compare Eq. (1) with another cross section, the Rosenbluth cross section:
$$ \left( \frac{\text{d}\sigma}{\text{d}\Omega} \right)_\text{Rosenbluth} = \left( \frac{\text{d}\sigma}{\text{d}\Omega} \right)_\text{Mott}\, \left[ \frac{1}{1+\tau}\big[G_E^2(Q^2) + \tau\, G_M^2(Q^2)\big] + 2\tau\,G_M^2(Q^2) \tan^2 \frac{\theta}{2} \right] $$
where $\tau=\frac{Q^2}{4m^2}$. (Notice the small $m$ since we need to distinguish the elastic ($m,x=1$) and inelastic ($M,0<x\leq 1$) case!) For pointlike particles, we have $G_E(Q^2)=1$ and $G_M(Q^2)=1$ and thus the Rosenbluth cross section becomes
$$ \left( \frac{\text{d}\sigma}{\text{d}\Omega} \right)_\text{Rosenbluth}^\text{(pointlike)} = \left( \frac{\text{d}\sigma}{\text{d}\Omega} \right)_\text{Mott}\, \left[ 1 + 2\tau\,\tan^2 \frac{\theta}{2} \right] \tag{2} $$
Since we know that we describe pointlike particles in Eq. (1), we can compare Eq. (1) to Eq. (2). We shall do this by considering the ratio of the magnetic part to the electric part:
$$ \begin{align} \frac{\text{magnetic part}}{\text{electric part}}\text{ in Eq. (1)} &= \frac{2\nu\,F_1(x,Q^2)\tan^2\frac{\theta}{2}}{M\, F_2(x,Q^2)} \tag{3a}\\ \frac{\text{magnetic part}}{\text{electric part}}\text{ in Eq. (2)} &= 2\tau\, \tan^2\frac{\theta}{2} = \frac{Q^2}{2m^2}\tan^2\frac{\theta}{2} \tag{3b} \end{align} $$
Since Eq. (3) corresponds to the elastic scattering case, we have the relation $Q^2=2m\nu$ (since $x=1$ here). We can use this to write
$$ \begin{align} \frac{\text{magnetic part}}{\text{electric part}}\text{ in Eq. (2)} &= \frac{2\nu^2}{Q^2}\tan^2\frac{\theta}{2} \tag{3b again} \end{align} $$
Let us now finally set Eqs. (3a) and (3b) equal:
$$ \frac{2\nu\,F_1(x,Q^2)\tan^2\frac{\theta}{2}}{M\, F_2(x,Q^2)} = \frac{2\nu^2}{Q^2}\tan^2\frac{\theta}{2} \tag{4}$$
As you can verify, using the definition of the Bjorken scaling $x=\frac{Q^2}{2M\nu}$, we can modify Eq. (4) to look like this:
$$ \frac{1}{2x}F_2(x,Q^2) = F_1(x,Q^2) $$
Actually, we have to include something: remember that I mentioned that for spin-0 particles, $F_1(x,Q^2)=0$? If we include this, we get:
$$ \frac{1}{2x}F_2(x,Q^2) = \begin{cases} 0 & \text{for spin-0}\\ F_1(x,Q^2) & \text{for spin-1/2} \end{cases} $$
And here we have it: since the proton's structure functions obey the lower equation, we can conclude that its constituents are in fact spin-1/2 particles!
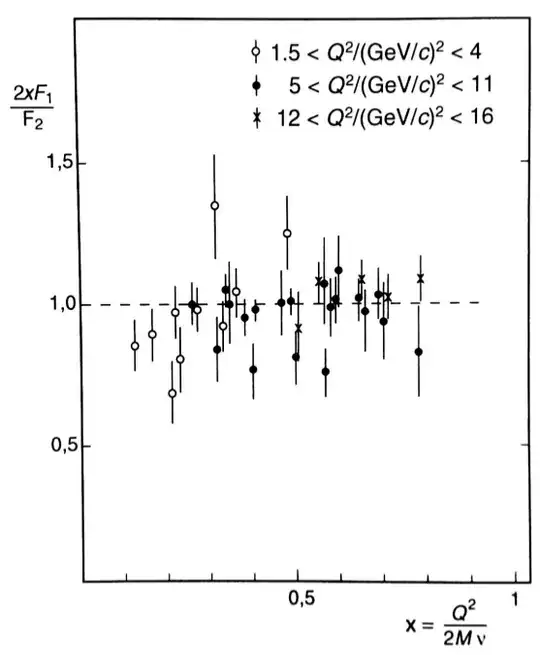
$^1$Density distribution and structure function are related by a Fourier transformation. If the structure function is almost constant w.r.t. $Q^2$, then the density distribution must be almost a delta function.
The Callan-Gross relation can also be understood in terms of helicity conservation.
Consider neutrino scattering which occurs via the exchange of a left-handed W boson. Write the structure functions NOT in the {F1,F2,F3} basis, but in the helicity basis: {Right, Left, Longitudinal} = {F+,F-,F0}.
You will find the left-handed structure function F- is proportional to the quarks, the right-handed structure function F+ is proportional to the anti-quarks (both with spin 1/2), and the longitudinal (scalar) structure function F0 is proportional to the SCALAR quarks (zero spin) if any existed.
Because there are no scalar quarks, then F0=0. In terms of {F1,F2,F3}, 2xF0 = F2 - 2xF1, so F0=0 implies F2= 2xF1.
This relation receives corrections due to quark masses (helicity is a Lorentz-invariant for massless but not for massive particles), and there will also be corrections at higher orders (especially from gluons).
