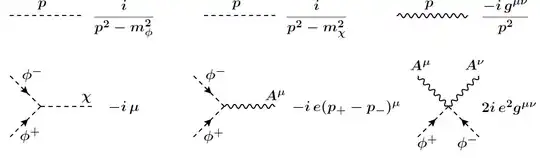
I'm having some difficulties regarding this problem in QFT I'm doing to prepare for an exam. For the following problem I consider the theory described by the Lagrangian: $$\mathcal{L}=-\frac{1}{4}F_{\mu\nu}F^{\mu\nu}-\frac{1}{2}(\partial_\mu A^\mu)^2+(\partial_\mu-ieA_\mu)\phi^-(\partial^\mu+ieA^\mu)\phi^++\frac{1}{2}\partial_\mu \chi\partial^\mu\chi-m^2_\phi\phi^+\phi^--\frac{1}{2}m^2_\chi\chi^2-\mu\phi^+\phi^-\chi$$
where $\chi$ is a neutral spin $0$ field, $\phi^\pm$ is a charged spin $0$ field and $A^\mu$ is the photon. The constant $e$ is the proton charge and $\mu$ has the dimensions of mass in natural units. This theory has the following propagators and vertices:
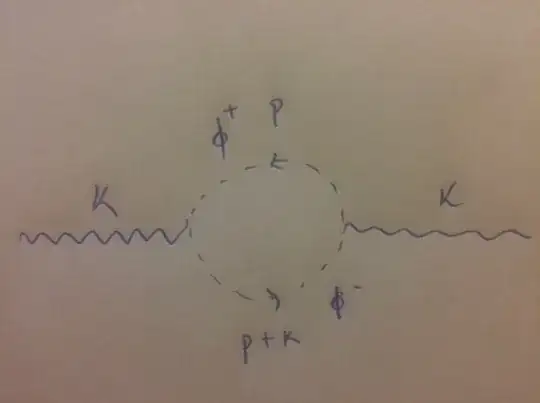
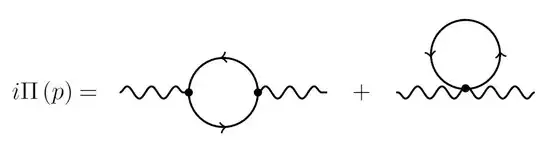
I'm considering the one-loop corrections in this model and only 1PI diagrams. I want to draw, for example, the diagrams that contribute to vacuum polarization of the photon and discuss its superficial degree of divergence. Here's where I want to check if I'm correct: for QED, we considered that electron-positron pairs are created as a "virtual" dipole that polarizes vacuum. In this case, since there are no vertices for charged fermions, but only for charged spin 0 bosons, then the diagram contributing for vacuum polarization in this case is only:
Am I correct? My second question is regarding the contribute to the one-loop correction to the vertex $\chi AA$, but I have no ideia how one corrects a vertex in this case: do we need to connect the photons, but with what?