There are two questions in one here:
Is it possible to concentrate mass more than is achieved by the horizon of a black hole?
Is it possible to concetrate mass more than is achieved by the singularity of a black hole?
The answer to (1) is "no" and the answer to (2) is "it is not known".
To expand:
(1). The Schwarzschild black hole has a spherical horizon whose area is equal to $4 \pi r^2$ where $r = 2 G M/c^2$ and $M$ is the mass of the black hole, as indicated by the amount of gravity it presents in the far-field or asymptotic limit. If further matter enters the hole in such a way that $M$ grows, then $r$ grows too, and it is not possible to concentrate a larger $M$ within a spherical surface of smaller surface area than this. (In this point of view we are associating the whole of $M$ with the region within the horizon, which is arguably correct for a Schwarzschild black hole, but it would not be correct for a black hole with angular momentum or electric charge or both.)
(2). The field equation of general relativity places no restriction on the amount of mass that can go into a black hole, and any mass that passes the horizon proceeds to the singularity in a finite amount of proper time. The singularity of a Schwarzschild black hole is spacelike, not timelike, so it is not quite right to think of it as having a volume. Rather, it is a sort of edge to spacetime.
Two further things are relevant.
First, as the mass gets larger, so does the horizon area, so such a black hole would have a horizon that swells to engulf a larger and larger proportion of the rest of the universe.
Secondly, general relativity employs a classical (i.e. not quantum mechanical) approach to physics, and this is known to fail when the scale of distance and momentum approaches the Heisenberg uncertainty limit. Therefore general relativity almost certainly no longer applies when the Schwarzschild radial coordinate is below some finite amount. In other words, the singularity will not be correctly described by general relativity.
We do not at present have a theory sufficiently well tested for us to have any confident knowledge of what happens at such a location in spacetime.
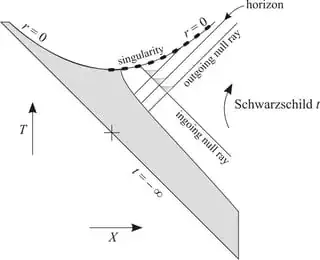
This diagram shows a spacetime in which a Schwarzschild black hole forms as a result of gravitational collapse of the matter shown in grey. The coordinates (Kruskal) have been chosen in such a way that horizontal lines are spacelike and vertical ones are timelike. I added the diagram in order to illustrate that in some sense the singularity has an infinite spatial length, yet it fits inside the horizon! One can also find a coordinate system in which the whole singularity is at one moment in time. The light cone above the horizon contains the singularity, but I would be unsure how to say what volume it has.
