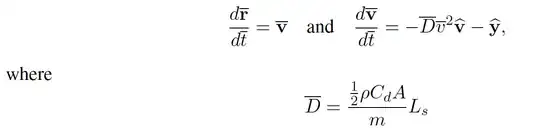Is Verlet method suitable for to solve projectile motion with quadratic drag?

Question

Consider the following non-dimensional equations of projectile motion in presence of air resistance,

I understand it can be numerically solved using the mid-point method, but can I also use Verlet method? Why midpoint method is more favourable in this case? Is this because the truncation error in velocity equation is of order $O(t^2)$ and $O(t^3)$ for position when midpoint method is used, which are $O(t^2)$ and $O(t^4)$ respectively when Verlet method is used? Am I thinking in the right direction?

Answer 1

The reason Verlet's algorithm is less suitable than midpoint method is due to the form of the force. Verlet's algorithm requires the acceleration at time step $t+\Delta t$ in order to update velocity at time $t+\Delta t$ (I refer to the so called "velocity" form of the algorithm, although the same considerations hold for the "position" form too): $$ \begin{eqnarray} x(t+\Delta t) &=& x(t) + v(t)\Delta t +\frac12 a(t) \Delta t^2 ~~~~~~~~~~~~~~[1]\\ v(t+\Delta t) &=& v(t) + \frac12\left( a(t) + a(t+\Delta t) \right) \Delta t ~~~~~~~~[2] \end{eqnarray} $$ If the force, and then the acceleration, depends on position only, $a(t+\Delta t) $ appearing in equation $[2]$ can be explicitly evaluated from the new position evaluated at $[1]$. However, if forces and then acceleration depend on velocities, equation [2] becomes an implicit equation for the velocity $v(t+\Delta t)$. It is simple to solve such equation in the case of linear forces (linear viscous friction or magnetic Lorentz force om a charged particle) but in the case of non-linear dependence on velocity things become more complex (and in 2D or 3D, much more complex) and usually other methods become preferable.