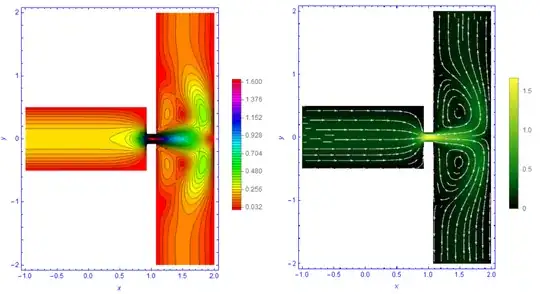
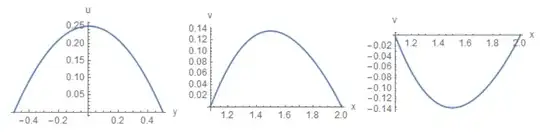
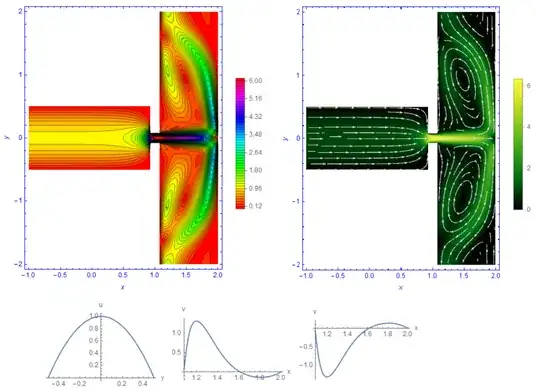
Well, the comments taken together are starting to look like an answer to your questions... so I'll collate them all here.
Is the only equation needed the one shown?
The answer is, unfortunately, no. You have written the steady, inviscid momentum equation for an incompressible flow. As noted in the comments, your velocity profiles and wall boundary conditions assume no-slip, and so you really need to add the viscous term to your equations. In theory, I suppose you could get away with the inviscid condition provided you specify that $u=0$ where all of your inflow/outflow boundaries meet the wall boundaries. That is probably similar to the Kutta Condition when solving for flow over airfoils. But it's certainly an odd choice and you'd be better served by including the viscous term, which will allow you to predict things like flow separation at the T-junction if it occurs.
The other thing to note is that your equation has 3 unknowns ($u$, $v$, $p$) and only 2 equations ($u$ and $v$). You might have thought that pressure is constant because density and temperature are constant. However, that only accounts for the thermodynamic component of pressure. There is still a dynamic component to pressure, which is proportional to $|\vec{u}|^2$.
So you need an additional equation. This equation is the Poisson equation for pressure. It is, unfortunately, elliptic and so it can't be solved easily with a marching scheme. Not a problem to implement, so long as you are careful in setting up your boundary conditions in the matrix and so long as you don't want to make this parallelized over many processors -- elliptic equations are hard to do that efficiently! You can see what this equation and derivation look like on this page, which also provides discrete forms of the important equations.
Speaking of boundary conditions, your choices on the outflows are... unconventional. Not going to say they won't work, but it might lead to a lot of convergence problems and possible divergence. I think you chose them to enforce that mass in == mass out. However, you can also enforce that by solving the continuity equation, $\vec{\nabla}\cdot \vec{u} = 0$. Then, your outflow conditions can be the standard zero-gradient in all variables, or perhaps zero-gradient for velocity and imposed pressure values. That's much more conventional.
Are there any hidden problems or further conditions I need to consider or specify
Boy are there. But, they are going to be mostly numerical. If you are going to use finite difference or finite volume methods, you have two choices on how to set up your discrete mesh. You can store and solve all of your variables at the same locations -- this is called a collocated approach. For FD methods, they collocated location is generally the nodes where grid lines intersect. For FV methods, it is the cell centers of the areas/volumes contained within intersecting grid lines. However, this will lead to nasty numerical instabilities and will fail to solve. This is because the stencil for the pressure equation and the stencil for the velocity equations will decouple and you'll get a checkboard pattern in your solution. To fix it, you need to add some sort of artificial dissipation. The Rhie-Chow interpolation scheme is the "classic" approach to fix this.
On the other hand, you can store your pressure and velocity at different locations. This is a staggered grid approach. This will give you proper coupling between the velocity and the pressure, and as a side-benefit, makes it much easier to enforce $\nabla \cdot u = 0$ where pressure is stored, because you can just compute the integral over the cell faces where the velocities are stored. However, it is much harder to keep track of the book-keeping in the code because now you need multiple index locations and arrays. It also does not easily extend to compressible flows, where staggered grids can be used but don't perform better than collocated grids.
For a summary I randomly picked off the internet, you can flip through these slides. I'm sure there are plenty more sources out there, but this can give you the terminology you need to search for things.
Somewhat counter-intuitively, unless you need to solve this particular problem for a particular reason, I would recommend learning how to write flow solvers by starting with supersonic flows over simple shapes. The flow is usually well approximated as inviscid, the equations are purely hyperbolic so you don't need to worry about elliptic solvers, you can either pseudo-time march to steady state or implicitly solve to steady state, and the equations are all coupled and can be treated as collocated. Plus the boundary conditions are the simplest possible.
So if you are just doing this to see how to do it, then that's where I would recommend starting. But, if you need this particular problem solved or you really want to give your programming muscles some work in addition to your fluid mechanics muscles, then what you have proposed is a good challange.