Is it correct to use Bernoulli's theorem to explain that a disk floats in the air? Should the correct explanation be based on Boyle's law?

Question

In this video, a device is introduced from 1 minute to 18 seconds. After entering the air, the disc at the bottom of the device will be suspended in the air. The video explains that this is because of the Bernoulli effect, but I think this explanation is incorrect, because the disc gap, the radial volume is increasing. Therefore, the reason why the disk is suspended is that the air volume becomes larger, so the pressure decreases (according to Boyle's law). If the air moves along the radial direction at a constant speed, the volume of the air must be constantly increasing, right? So the pressure is decreasing, right?

The disc is suspended in the air

Answer 1

In the case of an inviscid incompressible flow, the effect can be described using the Euler equations. Suppose that the flow velocity in the gap has one radial component $u_r=v(r)$. Then we have the continuity equation $$\frac {\partial (rv)}{\partial r}=0$$ and the Bernoulli equation $$p+\frac {\rho_0 v^2}{2}=p_0+\frac {\rho_0 v_0^2}{2}$$ Consequently, $rv=r_0v_0$ and the pressure distribution in the gap is defined as $$p =p_0+\frac {\rho_0 v_0^2}{2}(1-\frac {r_0^2}{r^2})$$ where $p_0,r_0,v_0$ are constants. Putting $r=R>>r_0$, where $R$ is the radius of the disk, and assuming that the pressure at the edge of the disk is equal to the atmospheric pressure $p_a$, we find $$p_a =p_0+\frac {\rho_0 v_0^2}{2}(1-\frac {r_0^2}{R^2})$$ Consequently, the pressure in the gap is $$p =p_a-\frac {\rho_0 v_0^2r_0^2}{2R^2}(\frac {R^2}{r^2}-1)<p_a$$ So we showed that the pressure in the gap less than atmospheric, which explains the effect. The Bernoulli integral describes the pressure distribution in an inviscid flow. In this case, the flow in a narrow gap is determined by viscosity. Using the Navier-Stokes equation, one can construct a numerical model and determine the distribution of pressure on the disk surface from the flow side. We take the atmospheric pressure for 1. If the pressure from the flow is less than 1, then this means that the external pressure presses the disk to the disk, and it explains the effect. In fig1. the geometry of the model and the distribution of pressure in the system and on the disk surface are shown. It is accepted that the flow is axisymmetric, laminar. Reynolds number = 100, Mach number = 0.1. From this data it follows that the pressure on the disk from the flow side is less than 1.

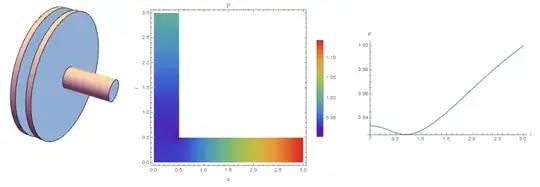
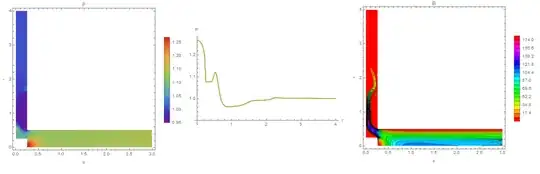
Consider the option when there is a protrusion on the lower disc, which partially closes the opening on the upper disc. In this case, a high-speed jet is formed in the gap, which leads to a drop in pressure below atmospheric. In fig. 2 shows the pressure distribution in the system and along the disk surface, as well as the analogue of the Bernoulli integral $$B=\frac {\rho u^2}{2}+p$$ The maximum Mach number is $M=0.42$,the atmospheric pressure $p_a=1$. In this case pressure integral $$\int_0^R{(p-p_a)ydy}<0$$ that is, a force acts on the lower disk, pressing against the upper disk, which explains the effect.