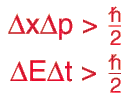According to the Uncertainty Principle we cannot calculate the precise position or momentum of a quantum particle at the same time, trying to calculate one of them would make the other uncertain. One of the examples is the Single Slit Experiment in which a photon or any other quantum particle passed through an extremely narrow slit is seen landing at multiple locations on the detecting screen on the other side of the slit, since we are certain about the position of particle passing through the slit we get an uncertainty in its momentum, the result of which is seen on the screen. My question is what if there is no scope given for the quantum particle to be uncertain of its position or momentum by constraining its motion in only one dimension i.e. instead of passing the particle through a single slit, what if we pass it through an infinitely long continuation of slits which are approximately of the size of quantum particle? In this way the particle would have no scope to obtain an uncertainty in momentum since it would have no place to land upon at multiple positions and hence the Uncertainty Principle would be violated?
3 Answers
According to the Uncertainty Principle we cannot calculate the precise position or momentum of a quantum particle at the same time, trying to calculate one of them would make the other uncertain.
This is a misunderstanding: not calculate, but measure.
The position and momentum of a particle cannot be simultaneously measured with arbitrarily high precision. There is a minimum for the product of the uncertainties of these two measurements. There is likewise a minimum for the product of the uncertainties of the energy and time.
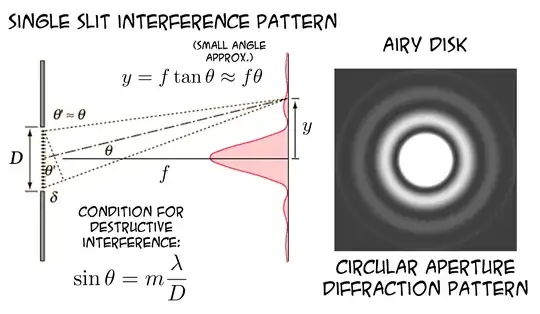
Since you are talking of single slits, here is what the interference pattern looks like:
The width of the slit is such as to conform with the energy of the electron so that the interference patterns would be visible.
The distribution on the right is the probability distribution of where a single electron will end up after passing the slit. You can see that maybe a fourth of the electrons will miss going through a second slit you want to set up. And that is a geometric progression. If you make the aperture smaller, less electrons will be going to the central peak.
My question is what if there is no scope given for the quantum particle to be uncertain of its position or momentum by constraining its motion in only one dimension i.e. instead of passing the particle through a single slit, what if we pass it through an infinitely long continuation of slits which are approximately of the size of quantum particle?
The probability of a particle passing through even 20 slits will be effectively zero.
The size of the quantum particle is its de Broglie wavelength, another rule of thumb that describes the probabilistic solutions of quantum mechanical entities.
The Heisenberg uncertainty is a rule of thumb way of talking of the way quantum mechanics constrains probabilities in interactions, in this case "electron hitting single slit".
- 236,935
Your proposed configuration limits further the position of the particle, but the more you constrain the position, the wider the approximation in momentum!
- 3,874
You seem to think that the uncertainty principle requires the uncertainty in position times the uncertainty in momentum to be equal to some amount. But that is not what the uncertainty principle says. It says that there is a constant such that the product of the uncertainty must be at least that constant. It does not violate the uncertainty principle for the product of the uncertainties to be more than that constant.
You also seem to be working without a precise definition of "uncertainty". Uncertainty, in this context, is simply another term for the standard deviation of the distribution. Even if there are an infinite number of places where the particle can be, that doesn't mean that there is infinite uncertainty. If the probabilities of locations far from the center go to zero fast enough, the total uncertainty will be finite. The normal distribution, for instance, has infinite spread, but finite standard deviation.
- 9,687