Iron can't exist in hydrodynamic equilibrium under the relevant conditions. We also observe at least some black holes whose masses are above the Tolman-Oppenheimer-Volkoff limit, so they can't be degenerate electron or neutron matter.
The best candidates for dark matter are WIMPs, and the best candidates among WIMPs are fermions. Under this suggestion, dark matter undergoing runaway gravitational collapse would be expected to form degenerate matter, much like a white dwarf or neutron star.
The Chandrasekhar limit is proportional to $m^{-2}$, where $m$ is the mass of the electron. Since dark matter particles have a mass greater than the mass of the electron, the Chandrasekhar limit for dark matter would be much lower, and therefore you're not going to get solar-mass degenerate-matter stars made of dark matter. (It would also be difficult to get such a thing to form by gravitational collapse.) I've spelled out the details of the estimate in more detail at the end of this answer.
Another popular dark matter candidate is the axion, which is a boson. Most models limit the mass of stable stars made out of axios to extremely small values. It does not appear possible to get these objects with the kinds of masses we see, for example, in Sag A*.
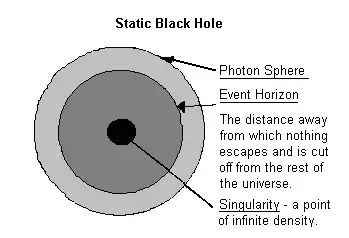
A singularity would break physics wouldn't it?
Not really. See Why exactly are singularities avoided or "deleted" in physics?
Details of the estimate for fermionic DM
Ignoring factors of $\pi$, etc., the pressure of a relativistic, degenerate gas is $P\sim hc(n/V)^{4/3}$. The pressure at the
core of the star is $P\sim GM^2/r^4$, where $M$ is the
total mass of the star. The star contains roughly equal numbers of
neutrons, protons, and electrons, so $M=Knm$, where $m$ is the mass of
the electron, $n$ is the number of electrons, and $K\approx 4000$. Setting the
pressure at the core equal to the degeneracy pressure of a
relativistic gas, we find that the Chandrasekhar
limit is $\sim (hc/G)^{3/2}(Km)^{-2}=6M_\odot$. This is ignoring factors of $\pi$, etc., but is still on the right order of magnitude, and I expect the dependence on the variables to be right. For a star made out of dark matter, we have $K=1$, but current estimates of the mass of WIMPs are in the range near about 10 GeV, or $2\times10^4 m_e$. This makes the factor $Km$ greater by something like a factor of 5, so that the Chandrasekhar limit should be smaller by about a factor of 25. Of course there is considerable uncertainty here, but it does seem sufficient to rule out the existence of stars made out of degenerate WIMP matter with masses greater than the white-dwarf version of the Chandrasekhar limit.