My original intuition was this:
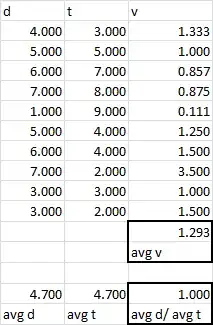
If you measured $x$ and $t$ once for each trial, then in your case $v$ is a function not a measurement. Every measurement generates its own pair of $x_i$ and $t_i$, which implies $v_i$. Thus you get $\hat v$ by averaging $v$. $x$ and $t$ depend on each other, as opposed to $x_i$-$x_j$, so it doesn't make sense to average $x_i$.
If you doubted your ability to precisely measure $x$ and $t$ (as well you should) then in each trial $i$ you would make $n$ measurements of $x_{ij}$. Now before you can do $v_i=x_i/t_i$, you must first have an estimate of $x_i$, which is given by $\frac{1}{n} \sum_j{x_{ij}}$. Thus you average $x$ for that trial, ditto $t$, get a $v_i$, repeat for each trial, and then average $v_i$.
However, I tried to simulate it and was surprised to find that it seems like there is hardly any difference. Below are sections of my R notebook along with results. Maybe I have a bug?
pacman::p_load(tidyverse, ggplot2)
Function to simulate an imprecise measurement:
# Relative measurement error
em = 0.01
measure = function(x, n) {
# Attempt to get the value of a quantity x, and n measurements
x_measured = mean(x*rnorm(n, 1, em))
return(x_measured)
}
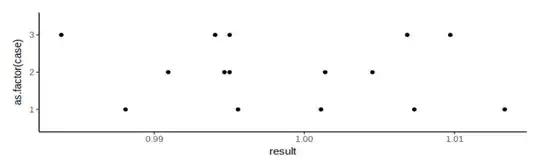
Let's test it with some simulated measurements:
df = expand.grid(case=1:3, measurement=1:5)
df$result = Vectorize(measure, vectorize.args = 'x')(replicate(nrow(df), 1), 1)
p = ggplot(df) +
geom_point(aes(y=result, x=as.factor(case))) +
theme_classic()
show(p)
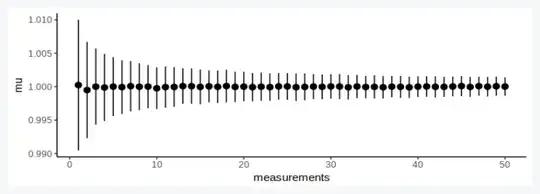
We expect repeated measurements to converge, but with diminishing returns:
df = expand.grid(case=1:1000, m=1:50)
df$result = Vectorize(measure, vectorize.args = 'n')(1, df$m)
df_sum = df %>% group_by(m) %>% summarise(mu = mean(result), sigma = sd(result), measurements = first(m))
p = ggplot(df_sum) +
# geom_boxplot(aes(y=result, x=measurements, group=measurements)) +
geom_pointrange(aes(x=measurements, y=mu, ymin=mu-sigma, ymax=mu+sigma)) +
theme_classic()
show(p)
We set up the ball experiment: The ball thrower has a velocity setting (the exact value of which we don't know) and the camera has a timer setting (the value of which we also don't know). So both v and t converge to one value, but have some experiment error. We try doing several experiments:
# Set ball roller to a certain energy level (value unknown to you)
v_expected = 5
# And the camera to photograph after a certain delay (value unknown to you)
t_expected = 20
# Relative apparatus error
ea = 0.001
# Number of trials
n = 10
# Number of experiments
k = 1000
df = expand.grid(experiment = 1:k, trial=1:n)
# Roll the ball for each trial, but the machine is slightly faster or slower sometimes
df$v_actual = v_expected*rnorm(nrow(df), 1, ea)
# The camera's timer isn't very consistent either
df$t_actual = t_expected*rnorm(nrow(df), 1, ea)
# We don't know the true distance yet, but nature does
df$x_actual = df$v_actual * df$t_actual
# Visualize
p = ggplot(df) +
geom_point(aes(x=x_actual, y=t_actual, color=v_actual), size=0.5) +
theme_classic()
show(p)
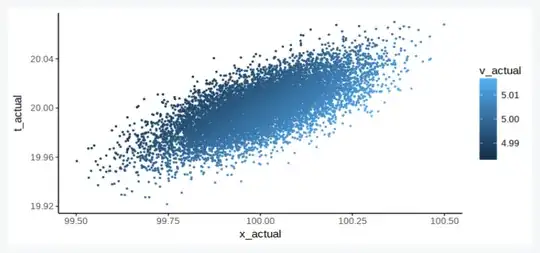
Now we try measuring our experimental outcomes:
# You try to measure the distance, but your ruler isn't very accurate
df$x_measured = Vectorize(measure, vectorize.args = 'x')(df$x_actual, 1)
# You also tried to measure the time, but your stopwatch is not the best
df$t_measured = Vectorize(measure, vectorize.args = 'x')(df$t_actual, 1)
# Number of repeat measurements
m = 20
# What if you measured x multiple times?
df$x_hat = Vectorize(measure, vectorize.args = 'x')(df$x_actual, m)
# And had multiple assistants, each with their stopwatches?
df$t_hat = Vectorize(measure, vectorize.args = 'x')(df$t_actual, m)
Of course multiple measurements are much better:
df_sum = df %>% gather(key='method', value='measurement', c(6,8)) %>%
mutate(error=abs(measurement-x_actual)/x_actual)
# Visualize
p = ggplot(df_sum) +
geom_boxplot(aes(x=method, y=error)) +
theme_classic()
show(p)
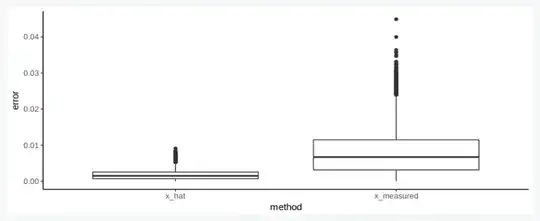
But does it matter when we average?
df_sum = df %>% mutate(v_measured = x_measured/t_measured) %>% group_by(experiment) %>%
summarise(v_bar = mean(v_actual),
t_bar = mean(t_actual),
x_bar = mean(x_actual),
v_bad = mean(x_measured)/mean(t_measured),
v_good = mean(v_measured),
v_best = mean(x_hat/t_hat),
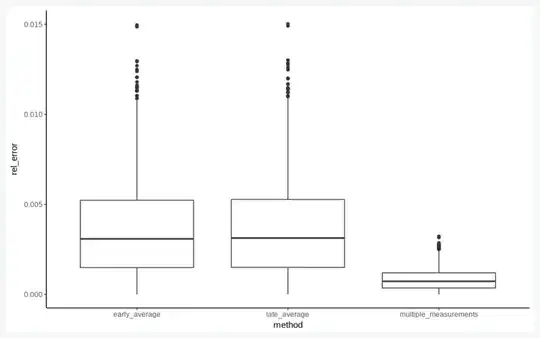
early = abs(v_bad-v_expected)/v_expected,
late = abs(v_good-v_expected)/v_expected,
multiple_measurements = abs(v_best-v_expected)/v_expected) %>%
gather(key='method', value='rel_error', 8:10)
df_sum$method = fct_inorder(df_sum$method)
# Visualize
p = ggplot(df_sum) +
geom_boxplot(aes(x=method, y=rel_error)) +
theme_classic()
show(p)