0

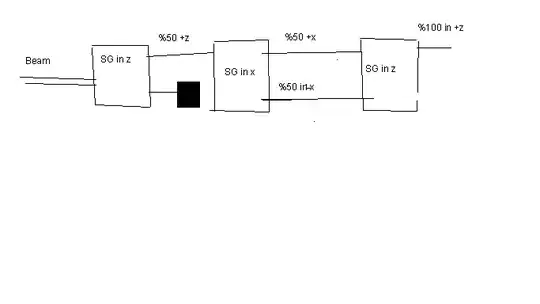
In quantum mechanics, in general, it is stated that the act of measurement changes the state of the system. For example, consider the following Stern-Gerlach setup;

A beam of silver atoms first passes through SG apparatus in $z$ direction. The ones come out from the +z direction are led to another SG apparatus that is in the $x$ direction. The ones come out from the +x direction are then led to yet another SG apparatus in the $z$ direction.

Now, if we were to perform this experiment, we would see that the silver atoms having spin in the +z direction, initially, can have a spin in the $-z$ direction at last apparatus.Therefore, as one of my professor put, the act of measuring the $x$ component of the spin erased the information about the component of the spin in the $z$ direction.

However, in the above experiment, we made a selection at the end of each apparatus; namely, we only allowed atom having spin $+z/+x$ to pass through the next stage, so consider the following;

enter image description here

In other words, in this case, we allow the atoms coming out from $-x$ direction pass to the next stage.

In this case, the act of measuring the $x$ component of the spin will not "erase" the information about the $z$ component (this experiment is explained in the QM lectures in ocw.mit.edu), so isn't the statement "the act of measurement changes the state of the system" wrong in general ?

Moreover, if we think about it, almost all of the "problematic" (weird) things in QM comes from the fact that by making a measurement, we cannot determine the state of a system priori to the measurement because by making a measurement, we are disturbing the system, hence we cannot talk about the state "priori to the measurement" by doing a measurement, but the latter experiment says "well you can actually in some cases", so I see a contradiction in here.

Edit:

Note that, in here, I'm consciously sending both output of $SG_x$ to the same $SG_z$ apparatus.

Community
  • 1
Our
  • 2,351
  • 19
  • 37

2 Answers2

2

In this case, there is no measurement of spin in the $x$-direction happening. You're just feeding the outcome of the $x$-aligned SG apparatus into the second $z$-aligned SG apparatus. But a measurement needs a "pointer" - something that indicates the result of measurement, otherwise it is not a measurement.

But there's nothing here that would force us to treat the outcome of the $x$-aligned SG apparatus as anything but an equal superposition of $\lvert -x\rangle$ and $\lvert x\rangle$, i.e. it's still just a $z$-spin eigenstate. Unless you introduce something in one of the two paths for the $x$-spins that distinguishes them, you're not forcing this superposition to resolve to a state with definite $x$-spin, and therefore you're not measuring the $x$-spin.

ACuriousMind
  • 132,081
0

Moreover, if we think about it, almost all of the "problematic" (weird) things in QM comes from the fact that by making a measurement, we cannot determine the state of a system priori to the measurement because by making a measurement, we are disturbing the system, hence we cannot talk about the state "priori to the measurement" by doing a measurement

Actually, there is what is called preparing a system and this means we fix the system to be in a definite state. This is done by measuring the system since this means that after the measurement it will be in the eigenstate associated with that measurement.

Mozibur Ullah
  • 14,713