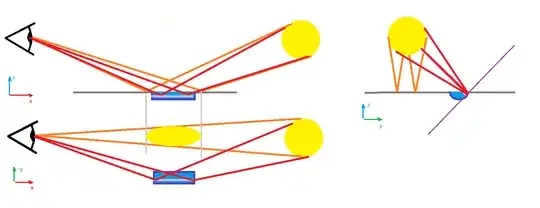
I assume you mean "tangential" instead of "axial" scratches. I made a few drawings as a visual aid. I know they are not exact and maybe crooked, but idealize them.
Okay, so first we've got the setup without scratches, should be simple enough. The top part represents the setup viewed from the side with $+y$ pointing towards us. The bottom part represents the setup viewed from the top with $+z$ pointing towards us.
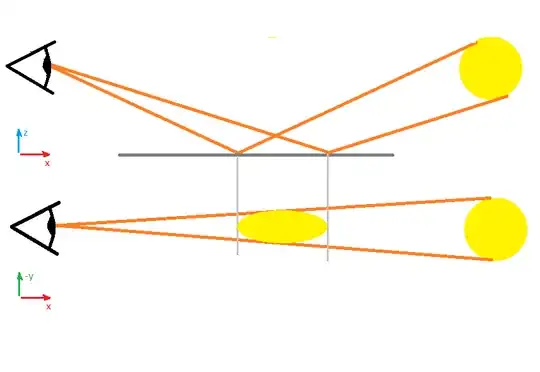
Second, we've got the setup with scratch that appears radial with respect to the reflection. The scratch is very exaggerated, appearing as a carving with a semi-elliptical profile. For us to see light in the scratch there must be a light source inbetween the red lines, but there is not.
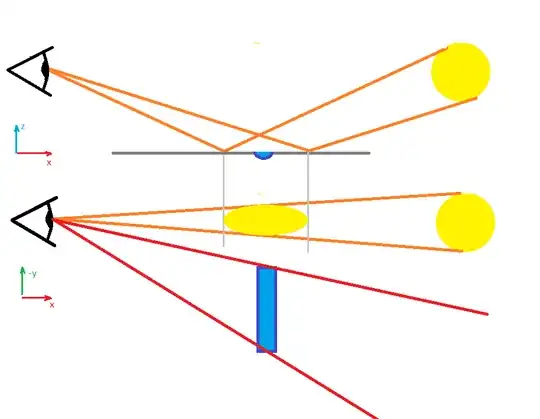
Third, we've got a scratch that would appear tangential with respect to the reflection (actually parallel to the tangent, because it is a bit to the side. I dont' know a term for this).
I've added a third point of view for this one. In this new point of view the coordinate that is pointing towards us is $+x$ such as the the observer (the eye) is "behind" the source. Again the scratch is exaggerated, with the same profile like the previous one. This time there is a portion of the arc of the ellipse that comes close to what orientation a reflective plane at that position would need to have to reflect the light from the source to the observer. In other words if there was a mirror, where the purple line is, in the point of view, given to the right, it would reflect the light from the source to the observer. A portion of the arc of the ellipse is close enough to simulate the mirror, so it reflects the light. The light beams that get reflected by the scratch I've colored in red. The strip of the scratch that is doing the reflecting I've colored in pink. In the additional point of view the the before being reflected by the scratch are the outer red ones. The middle red one is actually the already reflected beams, but they appear to coincide in my drawing.