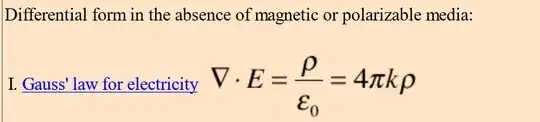1

In an earlier question, I asked about how to explain gravitational lensing to a layman in terms of propagating wave fronts, in a way analogous to the way an optical lens can be explained: the propagation velocity is inversely proportional to the refractive index of the glass and in the direction normal to the wavefront, which results in an initially plane wavefront being converted to a concave, converging wavefront.

Subsequently, I found several papers and presentations that described the vacuum as having an “effective refractive index” determined by the gravitational potential: (1), (2), (3), (4). The effective refractive index can then be used to explain gravitational lensing from either the ray perspective or the wave perspective.

This leads to a confusing inference, though, because dielectric constant is equal to the square of the refractive index (assuming that magnetic permeability is equal to 1). So, it seems that the vacuum around a gravitating mass must have an "effective dielectric constant" that varies with distance from the mass.

So far, so good. But Gauss' law

Maxwell equation

says that the effective charge of a charged particle depends on the dielectric constant of the vacuum surrounding it. If the dielectric constant is a function of distance $r$, then the effective charge is a function of distance.

This suggests, then, that radial dependence of the gravitational potential will cause the effective charge of a massive charged particle to vary with distance from the particle. (By the way, vacuum polarization [https://quantummechanics.ucsd.edu/ph130a/130_notes/node507.html] which is presumably an unrelated phenomenon, has a similar effect.)

However, answers and comments in response to this PhysicsSE question state emphatically that the divergence of E is zero in vacuum, regardless of the gravitational potential, according to the Einstein-Maxwell equations.

I suspect that the disconnect is due to the fact that derivation of the “effective refractive index” in (1), (2), (3), (4) assumes that space is flat. However, my confusion remains: it seems that a distant observer, ignorant of general relativity, would see a distance-dependent variation in the (effective) charge of a massive charged particle.

Is there a way out of this apparent contradiction?

S. McGrew
  • 25,240
  • 3
  • 32
  • 81

1 Answers1

2

The effective refractive index idea is not at all about electrodynamics, or dielectric constant, or anything like that. It is simply a nice way to calculate null geodesics. That is what it is, and that is all it is.

What you do is first pick coordinates where the metric is static and with the spatial part 'conformally flat' (i.e. equal to some function of $r$ multiplied by a Euclidean metric). It won't always be possible to do that, but if it possible, as for example with the exterior Schwarzschild metric, then you can proceed. Next you notice that (i.e. prove that) the null geodesics lie exactly where you would calculate light rays to go if you were to pretend that spacetime is flat and light moves at the coordinate speed of light in your chosen coordinates, i.e. at $c$ divided by a factor given by the metric. So you call that factor $n$, an 'effective refractive index', and away you go. The method is useful because it gives a very good intuition about the effects you are calculating, and because it allows you to draw on known results and methods in ray optics.

But, I repeat, this whole calculation is simply a way to find null geodesics in whatever spacetime you have; it does not have anything to do with electromagnetic fields or Maxwell's equations or permittivity. Having said that, this does not rule out that it might be possible to employ a similar style of reasoning to get insight into electromagnetic phenomena in curved spacetime in some situations. The idea is to spot when the GR equations happen to fall out in a way that can be interpreted as a field theory or particle theory in flat spacetime.

Andrew Steane
  • 65,285