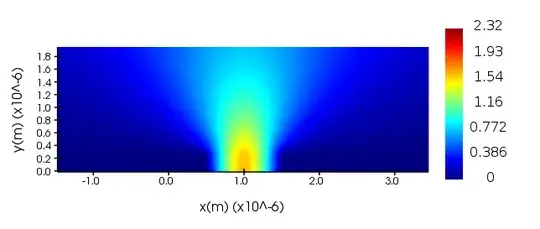
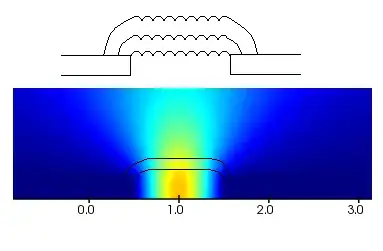
"Why are waves straight?" is the first question.
Let's start with a model of waves where particles don't have much kinetic energy. They just have potential energy.
Each location, if it has less energy than an adjacent spot, steals 1 unit of energy from it.
So if we start with:
00000
00000
00900
00000
00000
next tick:
00000
01110
01110
01110
00000
next tick:
0000000
0.111.0
0100010
0101010
0100010
0.111.0
0000000
0.....0
.00000.
.0...0.
.0.0.0.
.0...0.
.00000.
0.....0
where . is a fractional unit of energy.
and we see a really simple model of a "circlular wave" coming from a point.
Now look what happens when we have a wave-front (I'll assume the lines go off "forever" on the left and right, but there is a wall at the top).
0000000000000
9999999999999
0000000000000
0000000000000
0000000000000
0000000000000
0000000000000
0000000000000
3333333333333
3333333333333
3333333333333
0000000000000
0000000000000
0000000000000
0000000000000
0000000000000
3333333333333
3333333333333
0000000000000
3333333333333
0000000000000
0000000000000
0000000000000
0000000000000
3333333333333
0000000000000
5555555555555
0000000000000
1111111111111
0000000000000
0000000000000
0000000000000
0000000000000
4444444444444
0000000000000
4444444444444
0000000000000
1111111111111
0000000000000
0000000000000
3333333333333
0000000000000
2222222222222
0000000000000
3333333333333
0000000000000
1111111111111
0000000000000
hey look, waves. (I did some rounding) with some initial "sloshing" as it bounces off the "wall' at the top.
So suppose you have a bunch of waves causing a hole in a wall to go up and down:
######9######
0000000000000
0000000000000
0000000000000
0000000000000
######0######
0000033300000
0000000000000
0000000000000
0000000000000
######9######
0000100010000
0000111110000
0000000000000
0000000000000
######0######
0001033301000
0001000001000
0001111111000
0000000000000
because there is no intrinsic direction to the wave, just up and down, it induces a circular wave at the point of departure.
Being more mathematical, a linear wave is just a bunch of circular waves. Take 5 copies of this:
00000
00000
00900
00000
00000
offset by one horizontally and you get:
000000000
000000000
009999900
000000000
000000000
000000000
013333310
030000030
013333310
000000000
012333210
100000001
102000201
100000001
012333210
because the "hump" of 9s adjacent to each 9 slows inflow.
A real physical wave is more complex than this simple discrete time cell model. But the basic idea; that "humps" push water away and "gulfs" pull it in, and that there is enough momentum to cause overshoot -- result in a similar effect. Linear waves are the result of linear adjacent "humps" and "gulfs". When you reach a barrier with a hole, the linear "adjacent humps" go away, and the wave becomes more cicular as it falls both "forward" and "sideways", instead of being supported on the sides by other "humps" of water.
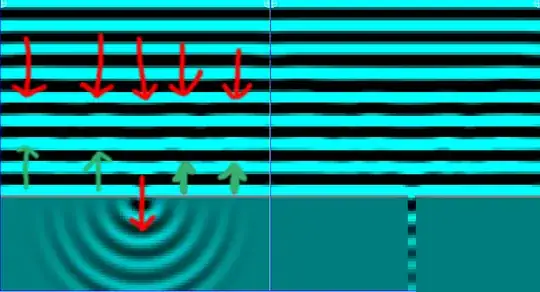 The waves that go in a straight direction should follow traveling straight line like a car that goes under a bridge the car is straight on the road.
But this is not so.
The waves that go in a straight direction should follow traveling straight line like a car that goes under a bridge the car is straight on the road.
But this is not so.