I read in a book named "Three Roads to Quantum Gravity" written by Lee Smolin that any accelerating body always have some hidden region of space-time from which light is never able to catch up with them, thus they develop some sort of an Event Horizon for themselves. Since any object possessing mass can never reach the speed of light, how is it possible for an accelerating object to never catch up with a ray of light?
2 Answers
The horizon that forms for a constantly accelerating frame in flat spacetime is a beautiful thing; it teaches all sorts of helpful lessons about G.R. I think the nicest way to appreciate it is to take a long look at the following diagram and the commentary that follows it:
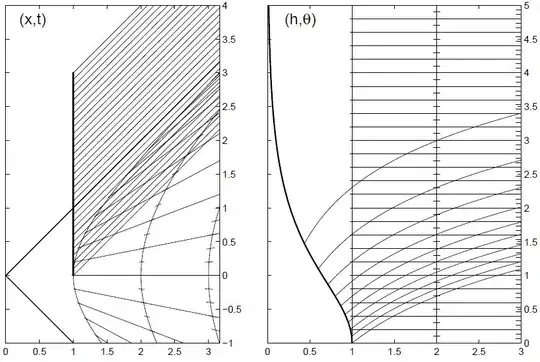
These two diagrams show the same region of spacetime. It is flat spacetime, so Special Relativity applies. On the left you have the usual way to treat it, using the $x,t$ coordinates of an inertial frame. The $t$ axis is vertical, the $x$ axis horizontal and we take $c=1$. On the right is shown the same events but using coordinates
$ h = (x^2 - t^2)^{1/2}, \;\;\;\;\;\;\; \theta = \tanh^{-1}(t/x) $
Various worldlines have been plotted. Lines at 45 degrees on the left diagram are photon worldlines; an example is the one setting out from $(0,0)$ and travelling to the right. The vertical line is the worldline of an object in constant velocity motion; think of it as a probe. It is sending out light signals which move away to its right. The curved lines with tick-marks are hyperbolas. Each one is the worldline of a particle moving at constant proper acceleration. The set of these particles can be thought of as the body of a rocket accelerating to the right. Notice that the photon emitted from $(0,0)$ never catches up with this rocket.
The straight lines with slope less than 45 degrees are lines that indicate sets of events that would be considered to be simultaneous for an observer sitting in the rocket.
Now look at the right hand diagram. It shows the same region of spacetime, but in the $(h,\theta)$ coordinate system. Each hyperbola from the first diagram is now straightened out into a vertical line, and each of the lines of simultaneity we just mentioned are now horizontal. It follows that, to an observer seated in the rocket, this diagram shows a natural way for him to interpret his surroundings. The various parts of the rocket are at a fixed 'distance' (i.e. $h$ coordinate) from one another (the straight vertical lines). The $\theta$ coordinate is a suitable measure of time passing, but notice the tick marks: a clock at a given height $h$ gives more ticks per unit change of $\theta$ when $h$ is large. This is the "gravitational time dilation". The tick marks show proper time, an observer low in the rocket considers that clocks at higher heights are ticking faster.
Finally, let's look at the signals sent out by the probe. This is where the discussion of the horizon comes in. The worldline of the probe is shown by the thicker curved line moving towards $h=0$ as $\theta$ increases. The photon signals have worldlines that are curved in the $h,\theta$ system (this illustates the effect of gravity on light). Look at the signals received by the observer sitting in the rocket at $h=1$. As time ($\theta$) goes on, the signals come more and more infrequently. And indeed, he never receives the photons sent out by the probe after the probe passes the right-going photon that we noticed in the first diagram. It is this photon worldline which marks the location of a horizon. No event to the left of this horizon can influence events to the right of it, nor can anything cross from left to right, not even light.
In the $h,\theta$ coordinate system, an infinite time $\theta$ has to pass before the probe actually reaches and crosses the horizon as the probe falls in, but this does not change the fact that the number of photons sent out before arriving at the horizon is agreed in the maps. The rocket observer thus agrees that the amount of proper time passing on the probe is not infinite, but the gravitational time dilation approaches infinity as the probe approaches the horizon. This is simply a statement about the relative calibration of two ways of keeping track of time: the proper time way and the $\theta$ way; both have their uses. Notice also that nothing special happens to the probe when it crosses the horizon. The horizon is itself a perfectly ordinary region of spacetime.
Finally, you should be thinking, "but doesn't this horizon appear and disappear, depending on choice of reference frame, whereas surely the horizon around a black hole is absolute?" This reservation is partially correct; it is to do with the difference between curved spacetime and flat spacetime. Even near the horizon of a black hole, I can if I like adopt an inertial frame---it is the frame of an object freely falling into the hole---and in this frame there will be no horizon. But such a frame cannot be extended very far in space and time; its 'map' of spacetime is rather local.
The singularity at the middle of the black hole is absolute, and so is the fact that a horizon encloses it in any coordinate frame able to extend through a spatial region that both contains the singularity and extends far from it.
The above diagram, and the ideas, are from "Relativity made relatively easy" (fig 9.20) , A. M. Steane (OUP 2012); this is an undergraduate physics textbook.
- 65,285
I've addressed this as a footnote to the question What is the proper way to explain the twin paradox? but since you are specifically asking about this point I'll post an answer here as well.
You need to know the equation that describes the trajectory of a uniformly accelerating object. The derivation isn't very illuminating so I'll content myself with quoting the result. For more details see Gravitation by Misner, Thorne and Wheeler chapter 6. There is also a summary in Phil Gibbs' excellent article on the relativistic rocket.
Anyhow, suppose you are accelerating with a constant proper acceleration $a$. Note that constant acceleration means the acceleration you feel in your rest frame is constant e.g. you feel a constant $1g$. The acceleration in the rest frame of the inertial observer watching you obviously can't be constant because that observer cannot see you exceed the speed of light. Suppose also that you start at the point $x = c^2/a$ at time $t=0$. In this case your distance as a function of time is given by:
$$ x = \frac{c^2}{a}\sqrt{1 + \left(\frac{at}{c}\right)^2} $$
We take a factor of $at/c$ out of the square root to get:
$$\begin{align} x &= \frac{c^2}{a}\frac{at}{c}\sqrt{1 + \left(\frac{c}{at}\right)^2} \\ &= ct\sqrt{1 + \left(\frac{c}{at}\right)^2} \end{align}$$
Now at time zero we send off a light beam from the origin $x=0$, so the light beam starts off a distance $c^2/a$ behind you. What we're going to show is that as long as you keep your constant acceleration $a$ the light beam can never catch you, and that means there is a coordinate horizon at the distance $c^2/a$ behind you.
To start with we'll simply reuse the last equation. We're interested in what happens at large times $t$, and when $t \gg c/a$ we have $c/at \ll 1$ so we can approximate our equation using the binomial theorem:
$$ x \approx ct\left(1 + \tfrac{1}{2}\left(\frac{c}{at}\right)^2\right) $$
Now the light starts at $x=0$and moves at a constant speed $c$, so the trajectory of the light is given by:
$$x_\text{light}=ct$$
And we get the distance between you and the light beam by subtracting the position of the light from your position:
$$\begin{align} x - x_\text{light} &\approx ct\left(1 + \tfrac{1}{2}\left(\frac{c}{at}\right)^2\right) - ct \\ &\approx \tfrac{1}{2}\left(\frac{c}{at}\right)^2 \end{align}$$
So what we find is that the light beam is always a distance $\tfrac{1}{2}(c/at)^2$ behind you i.e. the light ray can never catch you. This is why there is a horizon for a constantly accelerating observer.
- 107
- 367,598