Heisenberg energy uncertainty

Question

I am biologist and just new to the field of quantum mechanics and trying to understand the subject by reading. It is said that virtual particles are created due to the uncertainty of energy when consider a time, energy conjugate pair. Which leads to violate the energy conservation principle temporarily. But how a huge uncertainty in energy creates virtual particles? How it could violate the energy conservation principle?

Answer 1

This is an excellent question, which clearly demonstrated the lie perpetuated by a lot of people, that the Energy time uncertainty relationship has the same meaning as the momentum and position uncertainty relationship.

First of all, there is no energy and time uncertainty. Recall that the uncertainty principle for operators $\hat A$ and $\hat B$ have the form

$$ \sigma _ { A } \sigma _ { B } \geq \left| \frac { 1 } { 2 i } \langle [ \hat { A } , \hat { B } ] \rangle \right| = \frac { 1 } { 2 } | \langle [ \hat { A } , \hat { B } ] \rangle | $$

Now there is no "time" operator in quantum mechanics thus, it doesn't make any sense to talk about "time" uncertainty. The best you can do is the following for a time independent operator $\hat Q$:

$$\Delta \hat H \Delta t \geq \frac { \hbar } { 2 } , \quad \Delta t \equiv \frac { \Delta \hat Q } { \left| \frac { d \left< \hat Q \right> } { d t } \right| } $$

and this is what people mean, when they talk about Energy-time uncertainty. As you can see $\Delta t$ really has nothing to do with the "uncertainty in time", but rather is telling you roughly speaking, how big the uncertainty of an opeartor is compared to the variation of its expectation value.

Second thing you should know is that virtual particles also do not exist. They are essentially calculational tools that one uses for perturbation theory. The idea that two electrons see each other, "throw" a "virtual photon" and therefore repulse each other is atrocious. This view comes from overinterpreting Feynman diagrams, which are essentially pictures that simplify combinatoric calculations in perturbation theory. There is a beautiful epsiode by BPS Spacetime about virtual particles, if you want to learn more about virtual particles.

However, the upshot is that the statement that "virtual particles break conservation of energy for a very short time because of energy-time uncertainty principle" is devoid of meaning, as there is no virtual particles nor energy-time uncertainty principle.

Answer 2

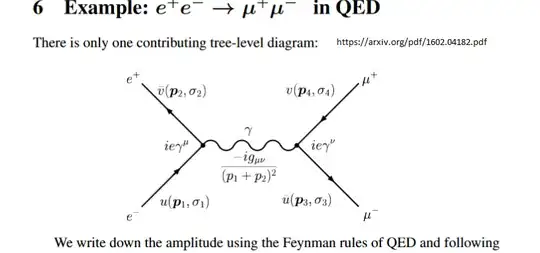
Virtual particles , as Gonenc Mogol says, are not particles, they are place holders for quantum numbers in the integrals necessary to calculate probabilities of interaction for quantum mechanical entities.

Here is a practical example :

The virtual particle is labeled as a photon, but in effect it is a place holder for the photon quantum numbers within an integral over the variables shown in the graph, it means that the photon is off mass shell, and the mass varies within the integration which will give real numbers ( note the imaginary numbers) to be compared with experiment. The link gives details . What can be measured are the input particle four vectors and the output particles four vectors, the internal lines, as the $γ$ here, are not accessible to measurement.

The popularization of this mathematical concept creates the confusion about uncertainties and energy conservation. In order to have virtual "particles" there must always be real energy input by incoming real particles, and real energy output by outgoing real particles. In between it is mathematics and hand waving misinterpretations.

Answer 3

It really depends on what you mean by conservation of energy. The classical idea is that the total energy is constant at all times. However, once quantum mechanics was discovered, people realized that our classical idea of conversation of energy is really just an approximation of the quantum conservation principle. In quantum mechanics, conservation of energy is a statement about the expectation value (think the average value) of energy; it says that the expectation value of energy does not change. Quantum fluctations in the energy cancel out over time, so the average energy of an isolated system never changes.

Effectively, physicists reformulated their idea about conservation of energy to agree with quantum mechanics, because they found that the classical notion breaks down.

As for how virtual particles are created, I'm not exactly sure. Somebody who is more familiar with QFT can probably answer.