Hello,
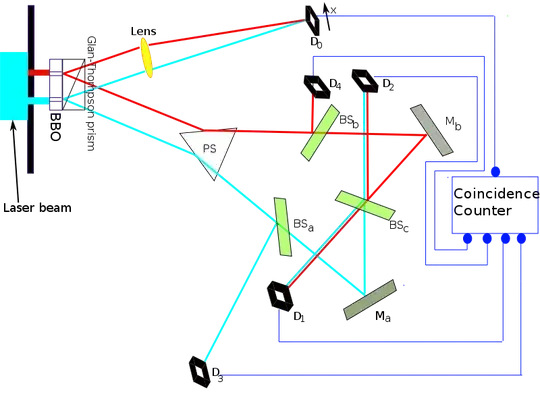
On the image above you'll find the display for the double slit "delayed choice quantum eraser" by Scully. I use this experiment for my question as it cames through trying to understand it.
The last part of the experiment on the right of the picture is a quantum eraser setup. When a Photon reach it the "which path information" is supposed to be lost.
But let be honest, it is impossible to make something absolutely perfectly symetrical. One of the red or blue path should be longer then the other (even by a tiny tiny tiny bit) For the purpose of this question let imagine the red is longer then the blue path by a time of T+x (where T is the time along the blue path).
If the photon take T time to reach D2 we know it was following the blue path, however if it takes T+x time we know it followed the red path... therefore the "which path information" is not really lost....
So how come that such quantum eraser still works?