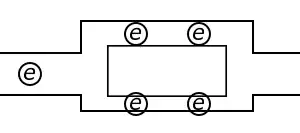
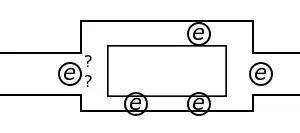
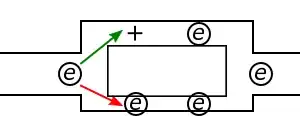
An electric charge will experience a force if an electric field is applied. If it is free to move, it will thus move contributing to a current. This is what the basic idea of 'Electric Currents in Conductors' is and this is apparently known to you. In nature, free charged particles do exist like in upper strata of atmosphere called the ionosphere. However, in atoms and molecules, the negatively charged electrons and the positively charged nuclei are bound to each other and are thus not free to move. Bulk matter is made up of many molecules a gram of water, for example, contains approximately $ 10^{22} $ molecules. These molecules are so closely packed that the electrons are no longer attached to individual nuclei. In some materials the electrons will still be bound, i.e., they will not accelerate even if an electric field is applied. In other materials, notably metals, according to the Drude-Lorentz Electron-sea theory, some electrons are practically free to move within the bulk material.
Resistance to electrical flow is due to the fact that when charge is given to a resistance, it remains stationary. In case of conductor, it is delocalised so it gets displaced and spread evenly on the surface, so note this carefully: in a conductor, charge flows mostly on the surface itself. This requires, undoubtedly some potential difference across the ends of the conductor but very less in magnitude. So, another fundamental rule/observation of universe is that "any dynamical process occurs in the path that requires least energy expense".
The most general and fundamental formula for Joule heating is:
$$ {\displaystyle P=(V_{A}-V_{B})I} $$
where
$P$ is the power (energy per unit time) converted from electrical energy to thermal energy,
$I$ is the current travelling through the resistor or other element,
${\displaystyle V_{A}-V_{B}}$ is the voltage drop across the element.
The explanation of this formula (P=VI) is:
(Energy dissipated per unit time) = (energy dissipated per charge passing through resistor) × (charge passing through resistor per unit time)
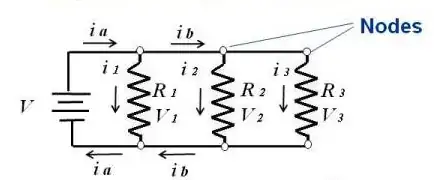
When Ohm's law is also applicable, the formula can be written in other equivalent forms:
$${\displaystyle P=IV=I^{2}R=V^{2}/R}$$
When current varies, as it does in AC circuits,
$${\displaystyle P(t)=U(t)I(t)}$$
where $t$ is time and $P$ is the instantaneous power being converted from electrical energy to heat. Far more often, the average power is of more interest than the instantaneous power:
$${\displaystyle P_{avg}=U_{\text{rms}}I_{\text{rms}}=I_{\text{rms}}^{2}R=U_{\text{rms}}^{2}/R}$$
where "avg" denotes average (mean) over one or more cycles, and "rms" denotes root mean square.
These formulas are valid for an ideal resistor, with zero reactance. If the reactance is nonzero, the formulas are modified:$${\displaystyle P_{avg}=U_{\text{rms}}I_{\text{rms}}\cos \phi =I_{\text{rms}}^{2}\operatorname {Re} (Z)=U_{\text{rms}}^{2}\operatorname {Re} (Y^{*})}$$
where $\phi$ is the phase difference between current and voltage,$Re$ means real part, $Z$ is the complex impedance, and Y* is the complex conjugate of the admittance (equal to $1/Z*$).
So, this shows how energy inefficient is electric flow through a resistance under an applied potential.